题目内容
【题目】已知△ABC中,BE平分∠ABC,点P在射线BE上.

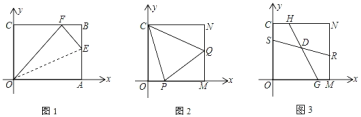
(1)如图1,若∠ABC=40°,CP∥AB,求∠BPC的度数;
(2)如图2,若∠BAC=100°,∠PBC=∠PCA,求∠BPC的度数;
(3)若∠ABC=40°,∠ACB=30°,直线CP与△ABC的一条边垂直,画出相应图形并求∠BPC的度数.
【答案】(1)∠BPC=20°;(2)∠BPC=100°;(3)画出相应图形见解析;∠BPC的度数为70°或40°或110°.
【解析】
(1)根据角平分线的定义与平行线的性质,即可求解;
(2)根据三角形内角和定理,可得∠A=∠BPC,进而即可求解;
(3)分3种情况:①当CP⊥BC时,②当CP⊥AC时, ③当CP⊥AB时,分别画出图形,即可求解.
(1)∵BE平分∠ABC,∠ABC=40°,
∴∠ABP=![]() =20°,
=20°,
∵CP∥AB,
∴∠BPC=∠ABP=20°;
(2)∵BE平分∠ABC,∠PBC=∠PCA
∴∠ABP=∠PBC=∠PCA
△ABO中,∠A+∠ABP+∠AOB=180°,
△PCO中,∠BPC+∠PCA+∠POC=180°,
∵∠ABP=∠PCA, ∠AOB=∠POC
∴∠A=∠BPC =100°
即∠BPC=100°;
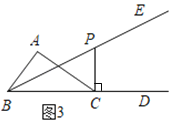
(3)①当CP⊥BC时,如图3,则∠BCP=90°,
∵∠PBC=20°,
∴∠BPC=70°;
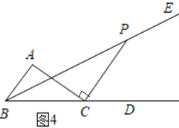
②当CP⊥AC时,如图4,则∠ACP=90°,
△BCP中,∠BPC=180°﹣20°﹣30°﹣90°=40°;
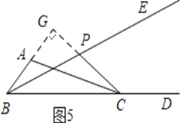
③当CP⊥AB时,延长CP交直线AB于G,如图5,则∠BGC=90°,
∵∠ABC=40°,
∴∠BCG=50°
△BPC中,∠BPC=180°﹣50°﹣20°=110°;
综上,∠BPC的度数为70°或40°或110°.

练习册系列答案
相关题目