题目内容
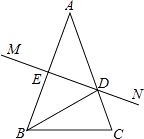
【题目】如图已知△ABE≌△ACD, AB=AC, BE=CD,∠B=40°,∠AEC=120°则∠DAC的度数为 ( )
A.80°
B.70°
C.60°
D.50°
【答案】A
【解析】
在△ABE中,利用外角的知识求出∠BAE的度数,再根据△ABC≌△ACD,得出∠BAE=∠DAC,这样即可得出答案.
由题意得:∠B=40°,∠AEC=120°,
又∵∠AEC=∠B+∠BAE(三角形外角的性质),
∴∠BAE=120°-40°=80°,
又∵△ABE≌△ACD,
∴∠BAE=∠DAC=80°.
故选A.
【考点精析】关于本题考查的三角形的外角和全等三角形的性质,需要了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;全等三角形的对应边相等; 全等三角形的对应角相等才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目