��Ŀ����
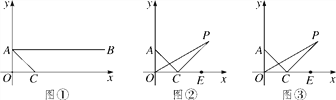
����Ŀ����ͼ������ƽ��ֱ������ϵ�У�A(0��1)��B(4��1)��CΪx����������һ�㣬��ACƽ����OAB.
(1)��֤����OAC����OCA��
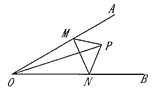
(2)��ͼ�������ֱ�����AOC�����ȷ�����OCA����ǵ����ȷ��߽��ڵ�P���������POC��![]() ��AOC����PCE��
��AOC����PCE��![]() ��ACE�����P�Ĵ�С��
��ACE�����P�Ĵ�С��
(3)��ͼ�ۣ���(2)�У�������OP��CP�����POC��![]() ��AOC����PCE��
��AOC����PCE��![]() ��ACE�������OPC�Ĵ�С����֤����Ľ���(�ú�n��ʽ�ӱ�ʾ)��
��ACE�������OPC�Ĵ�С����֤����Ľ���(�ú�n��ʽ�ӱ�ʾ)��
���𰸡���1��֤����������2��15�㣨3��![]()
�������������������1������AB���������á�OAB��С�����ݽ�ƽ�������ʿ���á�OAC��С�����ɽ��⣻
��2����������и����ġ�POC=![]() ��AOC����PCE=
��AOC����PCE=![]() ��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣻
��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣻
��3���ⷨ�ͣ�2����ͬ����������и����ġ�POC=![]() ��AOC����PCE=
��AOC����PCE=![]() ��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣮
��ACE������á�PCE�͡�POC�Ĵ�С���ٸ�����������ǵ��ڲ��������ڽǺͼ��ɽ��⣮
���������(1)֤������A(0��1)��B(4��1)����AB��CO�����OAB��180������AOC��90��.
��ACƽ�֡�OAB�����OAC��45�������OCA��90����45����45�������OAC����OCA.
(2)�⣺�ߡ�POC��![]() ��AOC�����POC��
��AOC�����POC��![]() ��90����30��.�ߡ�PCE��
��90����30��.�ߡ�PCE��![]() ��ACE�����PCE��
��ACE�����PCE��![]() (180����45��)��45��.�ߡ�P����POC����PCE�����P����PCE����POC��15��.
(180����45��)��45��.�ߡ�P����POC����PCE�����P����PCE����POC��15��.
(3)�⣺��OPC��![]() .
.
֤�����£��ߡ�POC��![]() ��AOC�����POC��
��AOC�����POC��![]() ��90����
��90����![]() .�ߡ�PCE��
.�ߡ�PCE��![]() ��ACE�����PCE��
��ACE�����PCE��![]() (180����45��)��
(180����45��)��![]() .
.
�ߡ�OPC����POC����PCE��
���OPC����PCE����POC��![]() .
.