题目内容
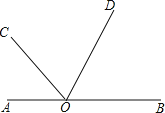
【题目】如图所示,直线AB、CD相交于点O,
(1)若∠AOC+∠BOD=90°,求∠BOC的度数
(2)若∠BOC比∠AOC的2倍多33°,求∠AOC的度数.
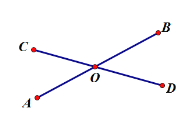
【答案】(1)135°;(2)49°.
【解析】
(1)根据对顶角相等,邻补角互补,∠AOC+∠BOD=90°,可得答案;
(2)根据邻补角互补,∠BOC比∠AOC的2倍多33°可得∠BOC与∠AOC的大小,根据对顶角相等,可得答案.
(1)由对顶角相等得出:∠AOC=∠BOD,
∵∠AOC+∠BOD=90°,
∴∠AOC=∠BOD=45°,
∴∠BOC=180°-45°=135°.
(2)由邻补角的性质,得∠BOC+∠AOC=180°,
由∠BOC比∠AOC的2倍多33°,得
∠BOC=2∠AOC+33°
2∠AOC+33°+∠AOC=180°
∴∠AOC=49°.

练习册系列答案
相关题目
【题目】如今,网上购物已成为一种消费常态,纪念日饰品店想购买一种贺年卡在元旦时销售,在互联网上搜索了甲、乙两家网店(如图所示),已知两家网店的贺年卡质量相同,请看图回答下列问题:
甲 网 店 | 鼎发贺年卡 ¥1.00 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个全部按六折 信用卡 最近售出11619个 |
乙 网 店 | 鼎发贺年卡 ¥0.80 产地:杭州 如实描述 信守天下 运费:8.00 七天退换 超过30个免运费 信用卡 最近售出10137个 |
(1)假如纪念日饰品店想购买x个贺年卡,那么在甲、乙两家网店分别需要花多少钱(用含x的式子表示)?(提示:如需付运费时,运费只需付一次,即8元)
(2)纪念日饰品店打算购买300个贺年卡,它应选择哪家网店省钱?