题目内容
 如图,一次函数y=
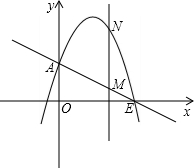
如图,一次函数y= 分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
分别交y轴、x 轴于A、B两点,抛物线y=-x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t 取何值时,MN有最大值?最大值是多少?
解:(1)∵一次函数y= 分别交y轴、x 轴于A、B两点,
分别交y轴、x 轴于A、B两点,
∴x=0时,y=2,y=0时,x=4,
∴A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,
将x=4,y=0,c=2代入y=-x2+bx+c,
得到b= ,
,
∴y=-x2+ x+2;
x+2;
(2)∵作垂直x轴的直线x=t,在第一象限交直线AB于M,
∴由题意,易得M(t,- t+2),N(t,-t2+
t+2),N(t,-t2+ t+2),
t+2),
从而得到MN=-t2+ t+2-(-
t+2-(- t+2)=-t2+4t (0<t<4),
t+2)=-t2+4t (0<t<4),
当t=- =2时,MN有最大值为:
=2时,MN有最大值为: =4.
=4.
分析:(1)首先求出一次函数与坐标轴交点坐标,进而带入二次函数解析式得出b,c的值即可;
(2)根据作垂直x轴的直线x=t,得出M,N的坐标,进而根据坐标性质得出即可.
点评:此题主要考查了一次函数与二次函数的综合应用,根据已知得出M,N的坐标是解题关键.
 分别交y轴、x 轴于A、B两点,
分别交y轴、x 轴于A、B两点,∴x=0时,y=2,y=0时,x=4,
∴A(0,2),B(4,0),
将x=0,y=2代入y=-x2+bx+c得c=2,

将x=4,y=0,c=2代入y=-x2+bx+c,
得到b=
 ,
,∴y=-x2+
 x+2;
x+2;(2)∵作垂直x轴的直线x=t,在第一象限交直线AB于M,
∴由题意,易得M(t,-
 t+2),N(t,-t2+
t+2),N(t,-t2+ t+2),
t+2),从而得到MN=-t2+
 t+2-(-
t+2-(- t+2)=-t2+4t (0<t<4),
t+2)=-t2+4t (0<t<4),当t=-
 =2时,MN有最大值为:
=2时,MN有最大值为: =4.
=4.分析:(1)首先求出一次函数与坐标轴交点坐标,进而带入二次函数解析式得出b,c的值即可;
(2)根据作垂直x轴的直线x=t,得出M,N的坐标,进而根据坐标性质得出即可.
点评:此题主要考查了一次函数与二次函数的综合应用,根据已知得出M,N的坐标是解题关键.

练习册系列答案
相关题目
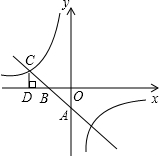 如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.此一次函数的解析式为
如图,一次函数与反比例函数的图象分别是直线AB和双曲线.直线AB与双曲线的一个交点为点C,CD⊥x轴于点D,OD=2OB=4OA=4.此一次函数的解析式为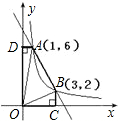 如图,一次函数y=-2x+b的图象与反比例函数
如图,一次函数y=-2x+b的图象与反比例函数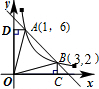 如图,一次函数y=-2x+b的图象与反比例函数
如图,一次函数y=-2x+b的图象与反比例函数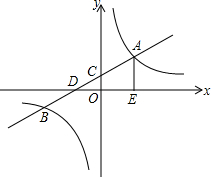 如图,一次函数y1=ax+2与反比例函数y2=
如图,一次函数y1=ax+2与反比例函数y2= 的[来源:Z*xx*k.Com]
的[来源:Z*xx*k.Com]