��Ŀ����
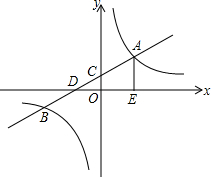 ��ͼ��һ�κ���y1=ax+2�뷴��������y2=
��ͼ��һ�κ���y1=ax+2�뷴��������y2=| k | x |
��1����a��k��ֵ��
��2������A��AE��x���ڵ�E����PΪ����������ͼ���λ�ڵ�һ�������ϵ�һ�㣬��ֱ��OP�֡�ADE���õ����������֮��Ϊ2��7����������з��������ĵ�P�����ꣻ
��3���ڣ�2���������£�����x������һ��Q��ʹ�á�PQC���ܳ���С���������Q�����꣮
��������1����B������뷴��������ʽ�����k��ֵ��ȷ��������������ʽ����B�������һ�κ�������ʽ���a��ֵ��ȷ����һ�κ�������ʽ��
��2��������������ǣ��ټ���P���ڣ�����OP����AE�ڵ�F����ͼ��ʾ����A������뷴��������ʽ�����m��ֵ��ȷ����A�����꣬�õ�AE��OE�ij�����һ�κ���y=0���x��ֵ��ȷ����D�����꣬�õ�OD�ij�����OD+OE���DE�ij�������ȷ����ֱ��������ADE���������������OEF��������ı���AFOD�����֮�ȣ����������OEF���������OE�ij������������������ʽ���FE�ij���ȷ����F���꣬��ֱ��OF����ʽΪy=kx����F����������k��ֵ��ȷ����ֱ��OF����ʽ���뷴��������ʽ�����������P�����꣬������������⣻�ڼ���P����ڣ�����OP��AC�ڵ�F����F��FH��x��ͬ���õ�������FDC���������OD���FH�ij���������֪һ�κ�������ʽ�У�ȷ����F���꣬�õ�F�ڵڶ����ޣ�����ͼ�Σ�ì�ܣ���ʱP�����ڣ����ϣ��õ���������P�����ꣻ
��3���ɣ�2���ó�P�����꣬�ҳ�P����x��ĶԳƵ�P�䣬����CP����x�ύ��Q�㣬������ɣ�
��2��������������ǣ��ټ���P���ڣ�����OP����AE�ڵ�F����ͼ��ʾ����A������뷴��������ʽ�����m��ֵ��ȷ����A�����꣬�õ�AE��OE�ij�����һ�κ���y=0���x��ֵ��ȷ����D�����꣬�õ�OD�ij�����OD+OE���DE�ij�������ȷ����ֱ��������ADE���������������OEF��������ı���AFOD�����֮�ȣ����������OEF���������OE�ij������������������ʽ���FE�ij���ȷ����F���꣬��ֱ��OF����ʽΪy=kx����F����������k��ֵ��ȷ����ֱ��OF����ʽ���뷴��������ʽ�����������P�����꣬������������⣻�ڼ���P����ڣ�����OP��AC�ڵ�F����F��FH��x��ͬ���õ�������FDC���������OD���FH�ij���������֪һ�κ�������ʽ�У�ȷ����F���꣬�õ�F�ڵڶ����ޣ�����ͼ�Σ�ì�ܣ���ʱP�����ڣ����ϣ��õ���������P�����ꣻ
��3���ɣ�2���ó�P�����꣬�ҳ�P����x��ĶԳƵ�P�䣬����CP����x�ύ��Q�㣬������ɣ�
����⣺��1����B��-8��-2�����뷴������������ʽ�ã�-2=
����ã�k=16��
��B��-8��-2������һ�κ�������ʽ�ã�-8a+2=-2����ã�a=
��
��2��������������ǣ�
����P����ڣ�����OP��AE�ڵ�F��
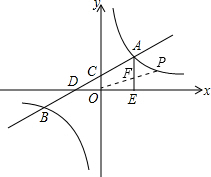
��A��4��m�����뷴��������ʽ�ã�m=4����һ�κ���y=
x+2�У�y=0����ã�x=-4��
��AE=4��OD=4��DE=OD+OE=4+4=8��
��S��ADE=
AE•DE=
��4��8=16��
�֡�S��OEF��S�ı���AFOD=2��7��
��S��OEF=
��16=
��
�֡�S��OEF=
EF•OE��OE=4��
��EF=
��
��F��4��
����
��ֱ��OF�ķ���Ϊy=kx����F��4��
������ã�k=
��
��ֱ��OF�����뷴������������ʽ�����ã�
��
��ã�
��
��
��P���ڵ�һ�����ڣ�
��P��6��
����
����P����ڣ�����OP��AC�ڵ�F����F��FH��x�ᣬ

��S��FDO��S�ı���ACOE=2��7��
��S��FDO=
��
��FH=y=
����y=
x+2�ã�x=-
��
��F��-
��
�����ڵڶ����ޣ�
��ͼ��ì�ܣ��ʴ�ʱP�㲻���ڣ�
���ϣ�P������Ϊ��6��
����
��3����P����ʱ��P��6��
������P�����x��ĶԳƵ�ΪP�䣨6��-
����
����P��C��x���ڵ�Q��

��P��C�ķ���Ϊy=kx+b����C��P���������ã�
��
��ã�
��
��P��C�ķ���Ϊy=-
x+2��
��y=0����ã�x=
��
��Q��
��0����
| k |
| -8 |
��B��-8��-2������һ�κ�������ʽ�ã�-8a+2=-2����ã�a=
| 1 |
| 2 |
��2��������������ǣ�
����P����ڣ�����OP��AE�ڵ�F��

��A��4��m�����뷴��������ʽ�ã�m=4����һ�κ���y=
| 1 |
| 2 |
��AE=4��OD=4��DE=OD+OE=4+4=8��
��S��ADE=
| 1 |
| 2 |
| 1 |
| 2 |
�֡�S��OEF��S�ı���AFOD=2��7��
��S��OEF=
| 2 |
| 9 |
| 32 |
| 9 |
�֡�S��OEF=
| 1 |
| 2 |
��EF=
| 16 |
| 9 |
��F��4��
| 16 |
| 9 |
��ֱ��OF�ķ���Ϊy=kx����F��4��
| 16 |
| 9 |
| 4 |
| 9 |
��ֱ��OF�����뷴������������ʽ�����ã�
|
��ã�
|
|
��P���ڵ�һ�����ڣ�
��P��6��
| 8 |
| 3 |
����P����ڣ�����OP��AC�ڵ�F����F��FH��x�ᣬ

��S��FDO��S�ı���ACOE=2��7��
��S��FDO=
| 32 |
| 9 |
��FH=y=
| 16 |
| 9 |
| 1 |
| 2 |
| 4 |
| 9 |
��F��-
| 4 |
| 9 |
| 16 |
| 9 |
��ͼ��ì�ܣ��ʴ�ʱP�㲻���ڣ�
���ϣ�P������Ϊ��6��
| 8 |
| 3 |
��3����P����ʱ��P��6��
| 8 |
| 3 |
| 8 |
| 3 |
����P��C��x���ڵ�Q��

��P��C�ķ���Ϊy=kx+b����C��P���������ã�
|
��ã�
|
��P��C�ķ���Ϊy=-
| 7 |
| 9 |
��y=0����ã�x=
| 18 |
| 7 |
��Q��
| 18 |
| 7 |
���������⿼���˷����������ۺ��⣬�漰��֪ʶ�У��ԳƵ����ʣ�������ͼ�����ʣ�����ϵ����ȷ����������ʽ��һ�κ�����������Ľ��㣬�Լ�һ�κ����뷴���������Ľ������⣬������ô���ϵ�����ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д�
�����Ŀ
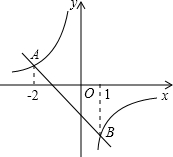 ��ͼ��һ�κ���y1=kx+b��ͼ���뷴��������y2=
��ͼ��һ�κ���y1=kx+b��ͼ���뷴��������y2=| m |
| x |
| A��-2��x��1 |
| B��0��x��1 |
| C��x��-2��0��x��1 |
| D��-2��x��1��x��1 |
 ��֪����ͼ��һ�κ���y1=kx+b��k��0����ͼ���뷴��������
��֪����ͼ��һ�κ���y1=kx+b��k��0����ͼ���뷴�������� ��ͼ��һ�κ���y1=kx+b��ͼ���뷴��������
��ͼ��һ�κ���y1=kx+b��ͼ���뷴�������� ��ͼ��һ�κ���y1=kx+1��k��0���뷴��������
��ͼ��һ�κ���y1=kx+1��k��0���뷴�������� ��ͼ��һ�κ���y1=kx+b�뷴��������y2=-
��ͼ��һ�κ���y1=kx+b�뷴��������y2=-