��Ŀ����
����Ŀ����ͼ1��������y=ax2+bx+ ![]() ����A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱ�������ABC��
����A��1��0����B��7��0�����㣬��y����D�㣬��ABΪ����x���Ϸ����ȱ�������ABC��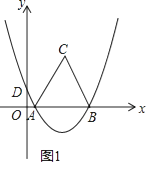
��1���������ߵĽ���ʽ��
��2����x���Ϸ������������Ƿ���ڵ�M����S��ABM= ![]() S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ABC�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
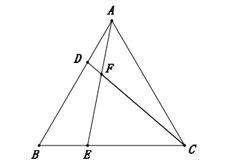
��3����ͼ2��E���߶�AC�ϵĶ��㣬F���߶�BC�ϵĶ��㣬AF��BE�ཻ�ڵ�P��
����CE=BF���Բ���AF��BE��������ϵ����APB�Ķ�������˵�����ɣ�
����AF=BE������E��A�˶���Cʱ����ֱ��д����P������·������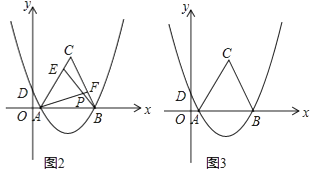
���𰸡�
��1���⣺����A��1��0����B��7��0�����������ߵĽ���ʽ�ã� 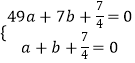 ��
��
��ã�a= ![]() ��b=��2��
��b=��2��
�������ߵĽ���ʽΪy= ![]() x2��2x+
x2��2x+ ![]() ��
��
��2���⣺���ڵ�M��ʹ��S��ABM= ![]() S��ABC��
S��ABC��
���ɣ���ͼ��ʾ������C��CK��x�ᣬ����ΪK��
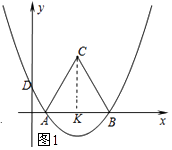
�ߡ�ABCΪ�ȱ������Σ�
��AB=BC=AC=6����ACB=60�㣮
��CK��AB��
��KA=BK=3����ACK=30�㣮
��CK=3 ![]() ��
��
��S��ABC= ![]() ABCK=
ABCK= ![]() ��6��3=9
��6��3=9 ![]() ��
��
��S��ABM= ![]() ��9
��9 ![]() =12��
=12��
��M��a�� ![]() a2��2a+
a2��2a+ ![]() ����
����
�� ![]() AB|y|=12����
AB|y|=12���� ![]() ��6����
��6���� ![]() a2��2a+
a2��2a+ ![]() ��=12��
��=12��
��ã�a1=9��a2=��1��
���M��������9��4����1��4����
��3���⣺�ٽ��ۣ�AF=BE����APB=120�㣮
�ߡ�ABCΪ�ȱ������Σ�
��BC=AB����C=��ABF��
���ڡ�BEC�͡�AFB�� 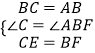 ��
��
���BEC�ա�AFB��
��AF=BE����CBE=��BAF��
���FAB+��ABP=��ABP+��CBE=��ABC=60�㣮
���APB=180�㩁60��=120�㣮
�ڵ�AE��BFʱ���ɢٿ�֪��P����ABΪֱ����Բ�ϣ�����M��ME��AB������ΪE��
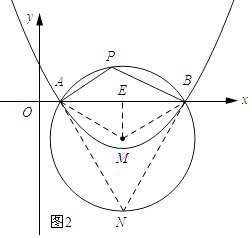
�ߡ�APB=120�㣬
���N=60�㣮
���AMB=120�㣮
�֡�ME��AB������ΪE��
��AE=BE=3����AME=60�㣮
��AM=2 ![]() ��
��
���P�˶���·��= ![]() =
= ![]() ��
��
��AE=BFʱ����P��AB�Ĵ�ֱƽ������ʱ����ͼ��ʾ������C��CK��AB�����P�˶���·��=CK�ij���
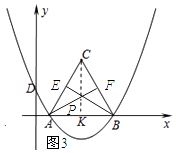
��AC=6����CAK=60�㣬
��KC=3 ![]() ��
��
���P�˶���·��Ϊ3 ![]() ��
��
������������P�˶���·��Ϊ3 ![]() ��
�� ![]() ��
��
����������1������A��B����������뺯������ʽ�����������飬������������ߵĽ���ʽ��
��2����֪��ABCΪ�ȱ������Σ�Ҫ��������ε���������Ӹ����ߣ�����C��CK��x�ᣬ�����ABC�ĸ�CK�ij����Ϳ��������ABC�����������S��ABM ��S��ABC�Ĺ�ϵ�����S��ABM��ֵ���ɵ�M��x���Ϸ����������ϣ������M�����꣬����S��ABM=12���������̣����������M�����ꡣ
��3���ٸ�����֪����֤�á�BEC�ա�AFB���ɵ�AF=BE����CBE=��BAF���������FAB+��ABP�Ķ�����������á�APB�������ڷ������������AE��BFʱ���ɢٿ�֪��P����ABΪֱ����Բ�ϣ�����M��ME��AB������ΪE������Բ�ڽ��ı��εĶԽǻ����������N�Ķ���������Բ�ܽǶ����������AMB�Ķ�����Ȼ�����E��ME��AB������ΪE���Ϳ������AM�ij������������P���˶�·��������AE=BFʱ����P��AB�Ĵ�ֱƽ������ʱ����ͼ��ʾ������C��CK��AB�����P�˶���·��=CK�ij�����Rt��AKC�У������KC�ij���
�����㾫�������ڱ��⿼��Ľ�ֱ�������Σ���Ҫ�˽���ֱ�������ε����ݣ��ٱߵĹ�ϵa2+b2=c2���ڽǵĹ�ϵ��A+B=90�㣻�۱߽ǹ�ϵ�����Ǻ����Ķ��壮(ע�⣺��������ʹ���м����ݺͳ���)���ܵó���ȷ�𰸣�

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�