题目内容
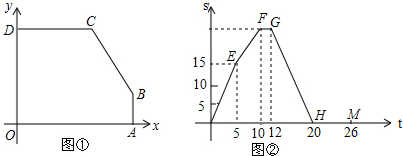
(2013•本溪一模)如图①,A,D分别在x轴,y轴上,AB∥y轴,DC∥x轴.点P从点D出发,以1个单位长度/秒的速度,沿五边形OABCD的边匀速运动一周,若顺次连接P,O,D三点所围成的三角形的面积为S,点P运动的时间为t秒,已知S与t之间的函数关系如图②中折线O′EFGHM所示.
(1)点B的坐标为
(2)若直线PD将五边形OABCD的周长分为11:15两部分,求PD的解析式.
(1)点B的坐标为
(8,2)
(8,2)
;点C的坐标为(5,6)
(5,6)
;(2)若直线PD将五边形OABCD的周长分为11:15两部分,求PD的解析式.

分析:(1)由于点P从点D出发,根据图②中S与t的图象可知,点P按顺时针方向沿五边形OABCD的边作匀速运动,又运动速度为1个单位长度/秒,所以DC=5,BC=5,AB=2,AO=8,OD=6,由此得到点C的坐标;过点B作BP⊥OD于P,过点C作CQ⊥BP于Q,根据矩形的性质、勾股定理求出点B的坐标;
(2)先求出五边形OABCD的周长为26,根据直线PD将五边形OABCD的周长分为11:15两部分,确定点P的位置有两种可能的情况:①在AB的中点;②在OA上,并且距离点A3个单位长度.再分别表示出点P的坐标,然后运用待定系数法求出PD的解析式.
(2)先求出五边形OABCD的周长为26,根据直线PD将五边形OABCD的周长分为11:15两部分,确定点P的位置有两种可能的情况:①在AB的中点;②在OA上,并且距离点A3个单位长度.再分别表示出点P的坐标,然后运用待定系数法求出PD的解析式.
解答: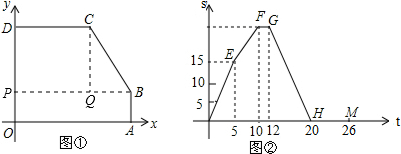 解:(1)由题意,可知点P的运动路线是:D→C→B→A→O→D,DC=5,BC=10-5=5,AB=12-10=2,AO=20-12=8,OD=26-20=6,所以点C的坐标为(5,6);
解:(1)由题意,可知点P的运动路线是:D→C→B→A→O→D,DC=5,BC=10-5=5,AB=12-10=2,AO=20-12=8,OD=26-20=6,所以点C的坐标为(5,6);
如图①,过点B作BP⊥OD于P,过点C作CQ⊥BP于Q,则四边形DCQP、ABPO均为矩形,PQ=DC=5,CQ=DP=OD-AB=6-2=4,
在Rt△BCQ中,∵∠BQC=90°,
∴BQ=
=
=3,
∴BP=BQ+PQ=3+5=8,
∴点B的坐标为(8,2);
(2)设PD的解析式为y=kx+b.
∵五边形OABCD的周长为:5+5+2+8+6=26,
∴直线PD将五边形OABCD的周长分为11:15两部分时,点P的位置有两种可能的情况:
①如果点P在AB的中点,那么DC+CB+BP=5+5+1=11,PA+AO+OD=1+8+6=15,点P的坐标为(8,1).
∵P(8,1),D(0,6),
∴
,解得
,
∴PD的解析式为y=-
x+6;
②如果点P在OA上,并且距离点A3个单位长度,那么DC+CB+BA+AP=5+5+2+3=15,PO+OD=8-3+6=11,点P的坐标为(5,0).
∵P(5,0),D(0,6),
∴
,解得
,
∴PD的解析式为y=-
x+6.
综上所述,PD的解析式为y=-
x+6或y=-
x+6.
故答案为(8,2),(5,6).
 解:(1)由题意,可知点P的运动路线是:D→C→B→A→O→D,DC=5,BC=10-5=5,AB=12-10=2,AO=20-12=8,OD=26-20=6,所以点C的坐标为(5,6);
解:(1)由题意,可知点P的运动路线是:D→C→B→A→O→D,DC=5,BC=10-5=5,AB=12-10=2,AO=20-12=8,OD=26-20=6,所以点C的坐标为(5,6);如图①,过点B作BP⊥OD于P,过点C作CQ⊥BP于Q,则四边形DCQP、ABPO均为矩形,PQ=DC=5,CQ=DP=OD-AB=6-2=4,
在Rt△BCQ中,∵∠BQC=90°,
∴BQ=
| BC2-CQ2 |
| 52-42 |
∴BP=BQ+PQ=3+5=8,
∴点B的坐标为(8,2);
(2)设PD的解析式为y=kx+b.
∵五边形OABCD的周长为:5+5+2+8+6=26,
∴直线PD将五边形OABCD的周长分为11:15两部分时,点P的位置有两种可能的情况:
①如果点P在AB的中点,那么DC+CB+BP=5+5+1=11,PA+AO+OD=1+8+6=15,点P的坐标为(8,1).
∵P(8,1),D(0,6),
∴
|
|
∴PD的解析式为y=-
| 5 |
| 8 |
②如果点P在OA上,并且距离点A3个单位长度,那么DC+CB+BA+AP=5+5+2+3=15,PO+OD=8-3+6=11,点P的坐标为(5,0).
∵P(5,0),D(0,6),
∴
|
|
∴PD的解析式为y=-
| 6 |
| 5 |
综上所述,PD的解析式为y=-
| 5 |
| 8 |
| 6 |
| 5 |
故答案为(8,2),(5,6).
点评:本题结合动点问题考查了矩形的性质,勾股定理,三角形的面积,五边形的周长,一次函数的图象与性质,运用待定系数法求一次函数的解析式等知识,综合性较强,难度适中.从函数图象中准确获取信息及利用分类讨论思想是解题的关键.

练习册系列答案
相关题目
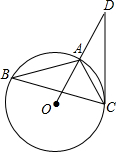 (2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
 (2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.
(2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.