题目内容
(2013•本溪一模)(1)已知,如图①,Rt△ABC∽Rt△AB′C′,相似比为k,∠ACB=∠AC′B′=90°,且∠A=30°,将△AB′C′绕点A逆时针旋转α后,点C′恰好在边BC的延长线上,如图②,若四边形ABB′C′是矩形,求α的度数及k的值;
(2)如图③,等腰△ABC∽等腰△AB′C′,相似比为k,AB=AC,AB′=AC′,∠A=36°,将△AB′C′绕点A逆时针旋转α后,点B′恰好在BC边的延长线上,如图④,若AC′∥BB′,①判断四边形ABB′C′的形状并说明理由;②α=
.

(2)如图③,等腰△ABC∽等腰△AB′C′,相似比为k,AB=AC,AB′=AC′,∠A=36°,将△AB′C′绕点A逆时针旋转α后,点B′恰好在BC边的延长线上,如图④,若AC′∥BB′,①判断四边形ABB′C′的形状并说明理由;②α=
72°
72°
,k=-1+
| ||
| 2 |
-1+
| ||
| 2 |

分析:(1)根据矩形的性质就可以求出∠C′AB=90°,进而求出a的值,由k=
=COS60°,就可以求出结论;
(2)由相似三角形的性质就可以求出∠CBA=∠C′B′A,由AB′=AC′就可以得出∠B′C′A=∠C′B′A,就有∠CBA=∠B′C′A,根据AC′∥BB′可以可以得出∠B′C′A+∠BB′C′=180°,就可以得出AB∥B′C′,得出四边形ABB′C′是平行四边形;就可以求出a的值,由相似三角形的性质就可以求出k的值.
| AC |
| A′C |
(2)由相似三角形的性质就可以求出∠CBA=∠C′B′A,由AB′=AC′就可以得出∠B′C′A=∠C′B′A,就有∠CBA=∠B′C′A,根据AC′∥BB′可以可以得出∠B′C′A+∠BB′C′=180°,就可以得出AB∥B′C′,得出四边形ABB′C′是平行四边形;就可以求出a的值,由相似三角形的性质就可以求出k的值.
解答:解:(1)∵四边形ABCD是矩形,
∴∠C′AB=90°,
∵∠A=30°,
∴a=∠C′AC=60°,
∴k=
=cos60°=
.
(2)①四边形ABB′C′是平行四边形.
理由:∵等腰△ABC∽等腰△AB′C′,
∴∠CBA=∠C′B′A.
∵AB′=AC′,
∴∠B′C′A=∠C′B′A,
∴∠CBA=∠B′C′A.
∵AC′∥BB′,
∴∠B′C′A+∠BB′C′=180°,
∴∠CBA+∠BB′C′=180°,
∴AB∥B′C′
∴四边形ABB′C′是平行四边形.
②∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵∠B+∠BAC+∠CAC′=180°,
∴∠CAC′=72°.
即a=72°.
如图④,∵72°+36°+36°+∠CAB′=180,
∴∠CAB′=36°,
∴∠AB′B=36°,∠BAB′=∠ABB′=72°
∴AC=B′C,AB′=BB′,△ABC∽△B′BA,
∴
=
.
设AB=x,AB′=BB′=a,
∴
=
,
∴BC=
.
∵BC+B′C=BB′=a,
∴
+x=a,
∴x2+ax-a2=0,
∴x1=
a(舍去),x2=
a,
∴AC=
a.
∴k=
=
.
故答案为:72°,
.
∴∠C′AB=90°,
∵∠A=30°,
∴a=∠C′AC=60°,
∴k=
| AC |
| AC′ |
| 1 |
| 2 |
(2)①四边形ABB′C′是平行四边形.
理由:∵等腰△ABC∽等腰△AB′C′,
∴∠CBA=∠C′B′A.
∵AB′=AC′,
∴∠B′C′A=∠C′B′A,
∴∠CBA=∠B′C′A.
∵AC′∥BB′,
∴∠B′C′A+∠BB′C′=180°,
∴∠CBA+∠BB′C′=180°,
∴AB∥B′C′
∴四边形ABB′C′是平行四边形.
②∵∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵∠B+∠BAC+∠CAC′=180°,
∴∠CAC′=72°.
即a=72°.
如图④,∵72°+36°+36°+∠CAB′=180,
∴∠CAB′=36°,
∴∠AB′B=36°,∠BAB′=∠ABB′=72°
∴AC=B′C,AB′=BB′,△ABC∽△B′BA,
∴
| AB |
| BB′ |
| BC |
| AB |
设AB=x,AB′=BB′=a,
∴
| x |
| a |
| BC |
| x |
∴BC=
| x2 |
| a |
∵BC+B′C=BB′=a,
∴
| x2 |
| a |
∴x2+ax-a2=0,
∴x1=
-1-
| ||
| 2 |
-1+
| ||
| 2 |
∴AC=
-1+
| ||
| 2 |
∴k=
| AC |
| AC′ |
-1+
| ||
| 2 |
故答案为:72°,
-1+
| ||
| 2 |
点评:本题考查了相似三角形的性质的运用,矩形的性质的运用,平行四边形的判定及性质的运用,三角函数值的运用,解答时证明三角形相似是关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
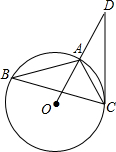 (2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
 (2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.
(2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.