题目内容
【题目】从正五边形的五个顶点中，任取四个顶点连成四边形，对于事件M：“这个四边形是等腰梯形” ．下列判断正确的是（ ）
A. 事件M是不可能事件 B. 事件M是必然事件
C. 事件M发生的概率为
D. 事件M发生的概率为
【答案】B
【解析】先得出从正五边形的五个顶点中，任取四个顶点连成四边形，一共有四种情况，再证明这四种都是等腰梯形，然后根据概率公式即可得出答案．
如图，
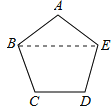
从正五边形ABCDE的五个顶点中，任取四个顶点连成四边形，可得到四边形BCDE，CDEA，DEAB，EABC，ABCD，一共四种情况．
连接BE．
∵五边形ABCDE是正五边形，
∴BC=DE=CD=AB=AE，
根据多边形的内角和（n-2）×180得：
∠A=∠ABC=∠C=∠D=∠AED=(5-2)×180°÷5=108°，
∴∠ABE=∠AEB=
（180°-∠A）=36°，
∴∠CBE=∠ABC-∠ABE=72°，
∴∠C+∠CBE=180°，
∴BE∥CD，
∴四边形BCDE是等腰梯形；
同理，可证四边形CDEA，DEAB，EABC，ABCD也都是等腰梯形，
∴这个四边形是等腰梯形的概率是
=1．
故选B．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
