题目内容
【题目】如图,在圆⊙O中,将弧AB沿弦AB折叠,使弧AB恰好经过圆心O,点P是优弧AMB上一点,则∠APB的度数为_________.
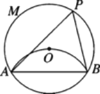
【答案】60o
【解析】分析:作半径OC⊥AB于D,连结OA、OB,如图,根据折叠的性质得OD=CD,则OD=![]() OA,根据含30度的直角三角形三边的关系得到∠OAD=30°,接着根据三角形内角和定理可计算出∠AOB=120°,
OA,根据含30度的直角三角形三边的关系得到∠OAD=30°,接着根据三角形内角和定理可计算出∠AOB=120°,
然后根据圆周角定理计算∠APB的度数.
如图,作半径OC⊥AB于D,连结OA、OB,
∵将⊙O沿弦AB折叠,圆弧恰好经过圆心O,
∴OD=CD,
∴OD= ![]() OC=
OC= ![]() OA,
OA,
∴∠OAD=30°,
又OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB= ![]() ∠AOB=60°
∠AOB=60°

故答案为120°.

练习册系列答案
相关题目