��Ŀ����
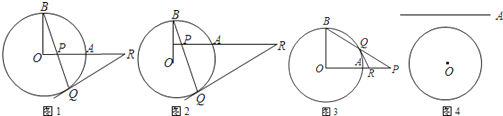
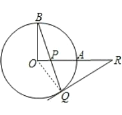
����Ŀ��������һ��ϰ�⣺��ͼ1����֪OA��OB�ǡ�O�İ뾶������OA��OB��P��OA����һ�㣨����O��A�غϣ���BP���ӳ��߽���O��Q����Q������O�����߽�OA���ӳ�����R��˵����RP=RQ����̽�����б仯��
�仯һ��������������ۣ�
��֪����ͼ1��OA��OB�ǡ�O�İ뾶������OA��OB��P��OA����һ�㣨����O��A�غϣ���BP���ӳ��߽���O��Q��R��OA���ӳ�����һ�㣬��RP=RQ��
��֤��RQΪ��O�����ߣ�
�仯�����˶�̽����
��1����ͼ2����OA����ƽ�ƣ��仯һ�еĽ��ۻ������𣿣�ֻ�轻���жϣ�
��2����ͼ3�����P��OA���ӳ�����ʱ��BP����O��Q������Q����O�����߽�OA���ӳ�����R��ԭ���еĽ��ۻ�������Ϊʲô��
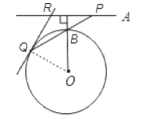
��3����OA���ڵ�ֱ������ƽ�������O�����㣬�������ԭ���е��������ͼ4�����жϽ����Ƿ�������ֻ�轻���жϣ�
���𰸡��仯һ�����������仯������1����OA����ƽ�ƣ��仯һ�еĽ��ۻ���������2��ԭ���еĽ��ۻ����������ɼ���������3��ԭ���еĽ��ۻ�����.
��������
ԭ�����֤��������OQ������RQΪ��O�����ߣ��ó���OQB+��PQR=90�������ݰ뾶OB=OQ��OA��OB���ó���OQB=��OBQ����OBQ+��BPO=90�����Ӷ��á�PQR=��QPR������ͬһ���������У��ȽǶԵȱߣ�֤������.
�仯һ��֤������ԭ�����֤�������෴����RP=RQ����֪��PQR=��QPR=��BPO����OB=OQ��OA��OB�ó���OQB=��OBQ����OBQ+��BPO=90���������û����ϵ���ǽ���ת����֤����OQB+��PQR=90��������OQR=90��������ɡ�OQR=90������֪RQΪ��O�����ߣ�
�仯����֤��������OQ������ԭ�����֤���������м���.
֤��������OQ��
��RQΪ��O�����ߣ�
���OQR=��OQB+��PQR=90����
�֡�OB=OQ��OA��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���PQR=��BPO��
����BPO=��QPR��
���PQR=��QPR��
��RP=RQ��
�仯һ��
֤������RP=RQ�����PQR=��QPR=��BPO��
�֡�OB=OQ��OA��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���OQB+��PQR=90��������OQR=90����
��RQΪ��O�����ߣ�
�仯����
��1����OA����ƽ�ƣ��仯һ�еĽ��ۻ�������
��2��ԭ���еĽ��ۻ�������
���ɣ�����OQ��

��RQΪ��O�����ߣ�
���OQR=90������BQO+��RQP=90����
�֡�OB=OQ��OP��OB��
���OQB=��OBQ����OBQ+��BPO=90����
���RQP=��BPO��
��RP=RQ��
��3��ԭ���еĽ��ۻ���������ͼ��

 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�