题目内容
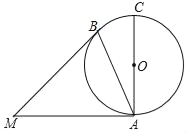
【题目】![]() 、
、![]() 为
为![]() 的切线,切点分别为点
的切线,切点分别为点![]() 、
、![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
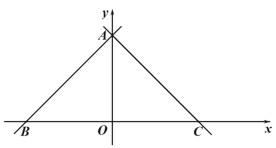
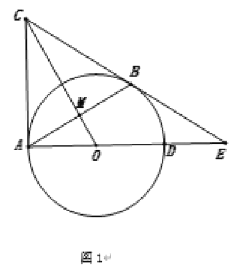
(1)如图1,求证:![]() ;
;
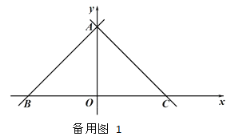
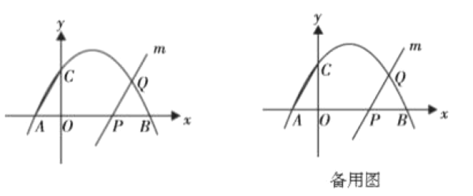
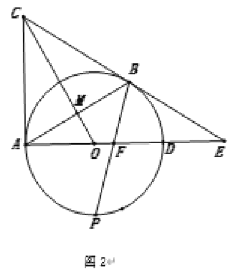
(2)如图2,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 交AD于点
交AD于点![]() ,求证:
,求证:![]() ;
;
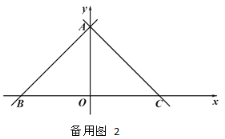
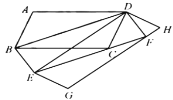
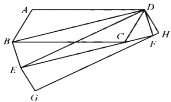
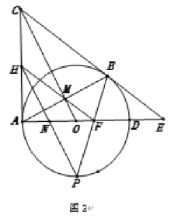
(3)如图3,在(2)的条件下:连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)由切线长定理可得CA=CB,∠ACO=∠BCO=![]() ∠ACB,∠CAO=90°,由等腰三角形的性质和余角的性质可得结论;
∠ACB,∠CAO=90°,由等腰三角形的性质和余角的性质可得结论;
(2)由等弧所对的圆周角相等可得∠ABP=∠DBP,由余角的性质和外角的性质可得∠EBF=∠BFE,可得BE=FE;
(3)如图3,连接BD,由全等三角形的性质和平行线分线段成比例可求BE=4,BC=AD=6=AC,OF=1,FD=2,AO=DO=3,以点A为原点,AE为x轴,AC为y轴,建立平面直角坐标系,分别求出直线FM,PH解析式,可求点H,点N的坐标,即可求解.
(1)∵CA、CB为⊙O的切线,切点分别为A、B,
∴CA=CB,∠ACO=∠BCO=![]() ∠ACB,∠CAO=90°,CO⊥AB,
∠ACB,∠CAO=90°,CO⊥AB,
∴∠CAM+∠ACM=90°,且∠CAM+∠BAO=90°,
∴∠BAO=∠ACM,
∴∠BAO=![]() ∠ACB;
∠ACB;
(2)连接BD,BO,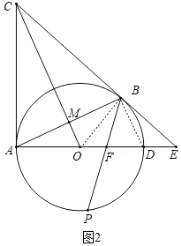
∵点P是弧AD的中点,
∴![]() =
= ![]() ,
,
∴∠ABP=∠DBP,
∵OA=OB,
∴∠OAB=∠OBA,
∵CE是⊙O切线,
∴∠OBE=90°,
∵AD是直径,
∴∠ABD=90°=∠OBE,
∴∠ABO=∠DBE=∠OAB,
∵∠EBF=∠PBD+∠DBE,∠BFE=∠OAB+∠ABF,
∴∠EBF=∠BFE,
∴BE=FE;
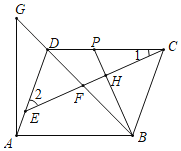
(3)如图3,连接BD,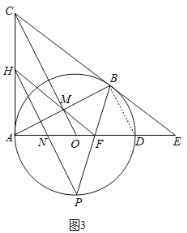
∵DF=2OF,
∴AO=DO=3OF,
∴AF=4OF,
∵∠ABP=∠PBD,
∴![]() ,
,
设BD=![]() ,则AB=
,则AB=![]() ,
,
∵OC⊥AB,
∴AM=BM=![]() AB=
AB=![]() =BD,
=BD,
∵AO=DO,AM=BM,
∴OM=![]() BD=
BD=![]() ,BD∥MO,
,BD∥MO,
∴∠BCO=∠DBE=∠OAB,且BM=BD,∠CMB=∠ABD=90°,
∴△CMB≌△ABD(AAS),
∴CM=AB=2![]() ,BC=AD,
,BC=AD,
∴CO=CM+OM=![]() ,
,
∵BD∥CO,
∴![]() ,
,
∴ ,
,
∴BE=4,
∴BC=CE-BE=6
∴BC=AD=6=AC,
∴AO=DO=3,OF=1,FD=2,
如图,以点A为原点,AE为![]() 轴,AC为y轴,建立平面直角坐标系,
轴,AC为y轴,建立平面直角坐标系,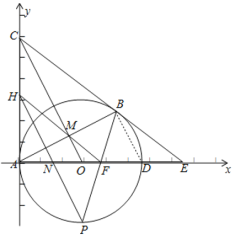
∴点A(0,0),点O(3,0)点C(0,6),点F(4,0),
∵⊙O半径AO=DO=3,且![]() =
=![]() ,
,
∴点P的坐标为(3,-3),
∵CO=CM+OM=![]() ,OM=
,OM=![]() ,CM=2
,CM=2![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴点M的坐标为(![]() ,
,![]() ),
),
设直线FM的解析式为![]() ,
,
∴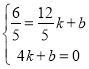 ,
,
解得: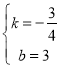 ,
,
∴直线FM的解析式为:![]() ,
,
∴点H坐标为(0,3),
设直线PH解析式为![]() ,
,
∴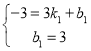 ,
,
解得: ,
,
∴直线PH解析式为:![]() ,
,
∴点N的坐标为(![]() ,0)
,0)
∴AH=3,AN=![]() ,
,
∴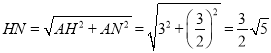 .
.

【题目】某中学为了了解“校园文明监督岗”的值围情况,对全校各班级进行了抽样调查,过程如下:
收集数据:从三个年级中随机抽取了20个班级,学校对各班的评分如下:
92 71 89 82 69 82 96 83 77 83
80 82 66 73 82 78 92 70 74 59
整理、描述数据:按如下分数段整理、描述这两组样本数据:
分数段 |
|
|
|
|
|
班级数 | 1 | 2 | a | 8 | b |
![]() 说明:成绩90分及以上为优秀,
说明:成绩90分及以上为优秀,![]() 分为良好,
分为良好,![]() 分为合格,60分以下为不合格
分为合格,60分以下为不合格![]()
分析数据:样本数据的平均数、中位数、众数、极差如下表,绘制扇形统计图:
平均数 | 中位数 | 众数 | 极差 |
79 | c | 82 | d |
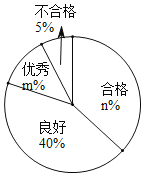
请根据以上信息解答下列问题:
![]() 填空:
填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______.
______.
![]() 若我校共120个班级,估计得分为优秀的班级有多少个?
若我校共120个班级,估计得分为优秀的班级有多少个?
![]() 为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励
为调动班级积极性,决定制定一个奖励标准分,凡到达或超过这个标准分的班级都将受到奖励![]() 如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由
如果要使得半数左右的班级都能获奖,奖励标准分应定为多少分?并简述其理由