题目内容
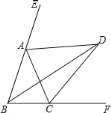
【题目】如图,在△ABC中,AB=AC=10,sinB=![]() ,
,
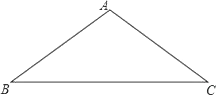
(1)求边BC的长;
(2)将△ABC绕着点C旋转得△A′B′C,点A的对应点A′,点B的对应点B′.如果点A′在BC边上,那么点B和点B′之间的距离等于多少?
【答案】(1)16(2)![]()
【解析】(1)AD⊥BC于点D,由等腰三角形的性质可得BC=2BD,在Rt△ABD中根据AD=ABsinB得出AD,再根据勾股定理即可得BD,从而得出答案;
(2)B′E⊥BC于点E,由旋转的性质得B′C=BC=16,∠ABC=∠ACB=∠A′CB′,在Rt△B′CE中求出B′E、CE的长,由BC=16可得BE的长,继而根据勾股定理可得答案.
(1)解:如图,过点A作AD⊥BC于点D,
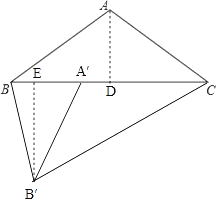
∵AB=AC=10,
∴BC=2BD,
在Rt△ABD中,∵sinB= ![]() ,
,
∴AD=ABsinB=10× ![]() =6,
=6,
∴BD= ![]() =8,
=8,
则BC=2BD=16;
(2)解:过点B′作B′E⊥BC于点E, 根据题意知B′C=BC=16,∠ABC=∠ACB=∠A′CB′,
∴sin∠BCB′=sinB= ![]() ,
,
∴B′E=B′Csin∠BCB′=16× ![]() =
= ![]() ,
,
∴CE= ![]() =
= ![]() ,
,
又∵BC=16,
∴BE=BC﹣CE=16﹣ ![]() =
= ![]() ,
,
∴BB′= ![]() =
= ![]() =
= ![]()

【题目】 某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 | 销售数量(盏) | 销售收入(元) | |
A品牌 | B品牌 | ||
第一天 | 2 | 1 | 680 |
第二天 | 3 | 4 | 1670 |
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
【题目】小张上星期六买进某公司的股票2000股,每股30元,下表是本周内每日该股票的涨跌情况(单位:元):
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股涨跌 |
|
|
|
|
|
|
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?
(3)请用拆线统计图表示该股票这六天的涨跌情况.(请在已设计好的坐标纸里画图)
(4)已知小张买过股票时付了1.5‰的手续费,卖出时需付成交额1.5‰的手续费和1‰的交易税,如小张在星期六收盘时将股票全部卖出,它的收益情况如何?