题目内容
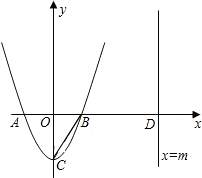
已知:如图,二次函数y=2x2-2的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,直线x=m(m>1)与x轴交于点D.(1)求A、B、C三点的坐标;
(2)在直线x=m(m>1)上有一点P(点P在第一象限),使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似,求P点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,试问:抛物线y=2x2-2上是否存在一点Q,使得四边形A
 BPQ为平行四边形?如果存在这样的点Q,请求出m的值;如果不存在,请简要说明理由.
BPQ为平行四边形?如果存在这样的点Q,请求出m的值;如果不存在,请简要说明理由.
分析:(1)令二次函数解析式中x=0,可得出C点坐标,令y=0,可得出A、B的坐标.
(2)由于∠PDB=∠BOC=90°,因此本题可分两种情况进行讨论:
①当△PDB∽△COB时;②当△PDB∽△BOC时;可根据不同的相似三角形得出的不同的对应线段成比例来求出DP的长,即可表示出P点的坐标.
(3)若四边形ABPQ为平行四边形,那么Q点的坐标可有P点坐标向左平移AB个单位来得出,然后将Q点坐标代入抛物线的解析式中即可求得m的值.
(2)由于∠PDB=∠BOC=90°,因此本题可分两种情况进行讨论:
①当△PDB∽△COB时;②当△PDB∽△BOC时;可根据不同的相似三角形得出的不同的对应线段成比例来求出DP的长,即可表示出P点的坐标.
(3)若四边形ABPQ为平行四边形,那么Q点的坐标可有P点坐标向左平移AB个单位来得出,然后将Q点坐标代入抛物线的解析式中即可求得m的值.
解答: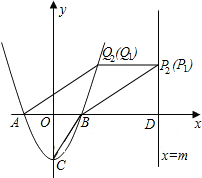 解:(1)令y=0得2x2-2=0
解:(1)令y=0得2x2-2=0
解得x=±1,
点A为(-1,0),点B为(1,0),
令x=0,得y=-2,
所以点C为(0,-2).
(2)当△PDB∽△COB时,有
=
,
∵BD=m-1,OC=2,OB=1,
∴
=
,
∴PD=2(m-1),
∴P1(m,2m-2).
当△PDB∽△BOC时,
=
,
∵OB=1,BD=m-1,OC=2,
∴
=
,
PD=
,
∴P2(m,
-
).
(3)假设抛物线y=2x2-2上存在一点Q,使得四边形ABPQ为平行四边形,
∴PQ=AB=2,点Q的横坐标为m-2.
当点P1为(m,2m-2)时,
点Q1的坐标是(m-2,2m-2)(9分)
∵点Q1在抛物线y=2x2-2图象上,
∴2m-2=2(m-2)2-2,m-1=m2-4m+4-1,
m2-5m+4=0,m1=1(舍去),m2=4.
当点P2为(m,
-
)时,
点Q2的坐标是(m-2,
-
),
∵Q2在抛物线y=2x2-2图象上,
∴
-
=2(m-2)2-2,
去分母,得
m-1=4(m-2)2-4m-1,
移项,得
4m2-16m+16-44m2-17m+13=0,
整理,得
(m-1)(4m-13)=0,
∴m3=1(舍去),m4=
,
∴m的值为4、
.
 解:(1)令y=0得2x2-2=0
解:(1)令y=0得2x2-2=0解得x=±1,
点A为(-1,0),点B为(1,0),
令x=0,得y=-2,
所以点C为(0,-2).
(2)当△PDB∽△COB时,有
| PD |
| OC |
| BD |
| OB |
∵BD=m-1,OC=2,OB=1,
∴
| PD |
| 2 |
| m-1 |
| 1 |
∴PD=2(m-1),
∴P1(m,2m-2).
当△PDB∽△BOC时,
| PD |
| OB |
| BD |
| OC |
∵OB=1,BD=m-1,OC=2,
∴
| PD |
| 1 |
| m-1 |
| 2 |
PD=
| m-1 |
| 2 |
∴P2(m,
| m |
| 2 |
| 1 |
| 2 |
(3)假设抛物线y=2x2-2上存在一点Q,使得四边形ABPQ为平行四边形,
∴PQ=AB=2,点Q的横坐标为m-2.
当点P1为(m,2m-2)时,
点Q1的坐标是(m-2,2m-2)(9分)
∵点Q1在抛物线y=2x2-2图象上,
∴2m-2=2(m-2)2-2,m-1=m2-4m+4-1,
m2-5m+4=0,m1=1(舍去),m2=4.
当点P2为(m,
| m |
| 2 |
| 1 |
| 2 |
点Q2的坐标是(m-2,
| m |
| 2 |
| 1 |
| 2 |
∵Q2在抛物线y=2x2-2图象上,
∴
| m |
| 2 |
| 1 |
| 2 |
去分母,得
m-1=4(m-2)2-4m-1,
移项,得
4m2-16m+16-44m2-17m+13=0,
整理,得
(m-1)(4m-13)=0,
∴m3=1(舍去),m4=
| 13 |
| 4 |
∴m的值为4、
| 13 |
| 4 |
点评:本题是二次函数的综合题,考查了二次函数的应用、相似三角形的判定和性质、平行四边形的判定和性质等知识.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
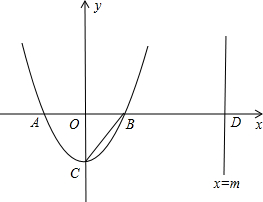 左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.
左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.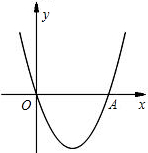 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点. 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: (2013•闸北区一模)已知:如图,二次函数
(2013•闸北区一模)已知:如图,二次函数 已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).