题目内容
【题目】如图,(10分)AB∥DE,试问∠B、∠E、∠BCE有什么关系.
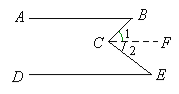
解:∠B+∠E=∠BCE
过点C作CF∥AB,
则![]() ____( )
____( )
又∵AB∥DE,AB∥CF,
∴____________( )
∴∠E=∠____( )
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
【答案】答案见解析
【解析】试题分析:关系为∠B+∠E=∠BCE,理由为:过点C作CF∥AB,理由两直线平行,内错角相等得到∠B=∠1,再利用平行于同一条直线的两直线平行得到DE与CF平行,利用两直线平行内错角相等得到∠E=∠2,利用等式的性质得到∠B+∠E=∠1+∠2,等量代换即可得证.
试题解析:∠B+∠E=∠BCE,
理由为:过点C作CF∥AB,∠B=∠1(两直线平行,内错角相等),
又∵AB∥DE,AB∥CF,
∴DE∥CF(平行于同一条直线的两直线平行),
∴∠E=∠2(两直线平行,内错角相等),
∴∠B+∠E=∠1+∠2,
即∠B+∠E=∠BCE.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目