题目内容
解方程时,把某个式子看成整体,用新的未知数去代替它,使方程得到简化,这叫换元法.先阅读下面的解题过程,再解出右面的方程:
例:解方程:2
-3=0
解:设
=t(t≥0)
∴原方程化为2t-3=0
∴t=
而t=
>0
∴
=
∴x=
请利用上面的方法,解方程 x+2
-8=0.
例:解方程:2
| x |
解:设
| x |
∴原方程化为2t-3=0
∴t=
| 3 |
| 2 |
| 3 |
| 2 |
∴
| x |
| 3 |
| 2 |
∴x=
| 9 |
| 4 |
请利用上面的方法,解方程 x+2
| x |
分析:设
=t,则原方程即可化成一个关于t的一元二次方程,解方程求得t的值,即
的值,然后平方即可求得x的值.
| x |
| x |
解答:解:设
=t(t≥0),
∴原方程化为t2+2t-8=0,
∴(t+4)(t-2)=0,
∴t1=-4(舍去),t2=2,
∴
=2,
∴x=4,
| x |
∴原方程化为t2+2t-8=0,
∴(t+4)(t-2)=0,
∴t1=-4(舍去),t2=2,
∴
| x |
∴x=4,
点评:本题考查了无理方程的解法,在解无理方程是最常用的方法是两边平方法及换元法,本题应用了换元的方法.

练习册系列答案
相关题目
 .
.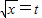 (t≥0)
(t≥0)



 (2)
(2)