Question

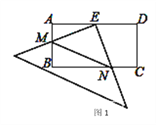
【题目】如图1，在△ABC中，AB=AC，D为BC边上一点，DE⊥AB于E，DF⊥AC于F．

作图：

（1）请作出AC边上的高BG．

探究：

（2）请你通过观察、测量找到DE、DF、BG之间的数量关系： ；

（3）为了说明DE、DF、BG之间的数量关系，小嘉是这样做的：

连接AD，则S△ADC= ，S△ABD= ，∴S△ABC= ，S△ABC还可以表示为 …

请你帮小嘉完成上述填空：

拓展：

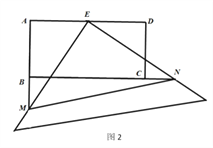
（4）如图2，当D在如图2的位置时，上面DE、DF、BG之间的数量关系是否仍然成立？并说明理由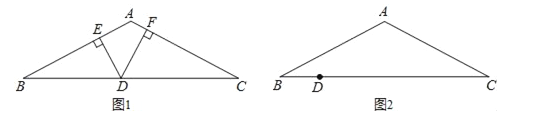

Answer 1

【答案】（1）答案见解析；（2）BG=DE+DF；（3）答案见解析；（4）成立．

【解析】试题分析：（1）按要求作出AC边上的高BG即可；

（2）连接AD，分别求出△ABD、△ADC与△ABC的面积，进而可得出结论；

（3）根据（2）中的过程即可得；

（4）根据（2）中的证明过程可得出结论．

试题解析：（1）如图所示：

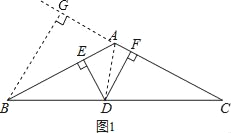
（2）BG=DE+DF，

连接AD，

∵DE⊥AB于E，DF⊥AC于F，AB=AC，

∴S△ABC=S△ABD+S△ACD=ABDE+ACDF=AC（DE+DF），

∵BG⊥AC，

∴S△ABC=ACBG，

∴BG=DE+DF，

故答案为：BG=DE+DF；

（3）由（2）可知，S△ADC=ACDF，S△ABD=ABDE，

∴S△ABC=ACDF+ABDE，

S△ABC还可以表示为ACBG，

故答案为： ACDF， ABDE， ACDF+ABDE， ACBG；

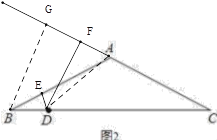
（4）拓展结论仍然成立，即BG=DE+DF，

连接AD，

∵DE⊥AB于E，DF⊥AC于F，AB=AC，

∴S△ABC=S△ABD+S△ACD=ABDE+ACDF=AC（DE+DF），

∵BG⊥AC，

∴S△ABC=ACBG，

∴BG=DE+DF.