题目内容
如图，在△ABC中，AB=AC，∠BAC=120°，AD是BC边上的中线，M为AC上一点，且CM=CD，求∠ADM的度数．
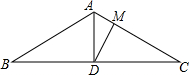
在△ABC中，AB=AC，∠BAC=120°，
∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
又∵CM=CD，
∴∠CDM=∠CMD=
×（180°-30°）=75°，
∵AB=AC，BD=CD，
∴AD⊥BC，即∠ADC=90°，
∴∠ADM=∠ADC-∠CDM=90°-75°=15°．
∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°，
又∵CM=CD，
∴∠CDM=∠CMD=
| 1 |
| 2 |
∵AB=AC，BD=CD，
∴AD⊥BC，即∠ADC=90°，
∴∠ADM=∠ADC-∠CDM=90°-75°=15°．
练习册系列答案
名校课堂系列答案
相关题目
