Question

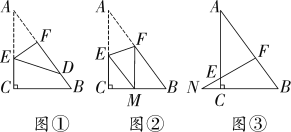
【题目】矩形纸片ABCD，AB=7，BC=4，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E、F，则EF=__________________．

Answer 1

【答案】或

【解析】

如图1，当点P在CD上时，由折叠的性质得到四边形PFBE是正方形，EF过点C，根据勾股定理即可得到结果；如图2当点P在AD上时，过E作EQ⊥AB于Q，根据勾股定理得到PB的长，推出△ABP∽△EFQ，列比例式即可得到结果．

如图1，当点P在CD上时，

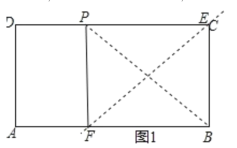
∵PD=3，CD=AB=7，

∴CP=4，

∵EF垂直平分PB，

∴四边形PFBE是正方形，EF过点C，

∴EF=

如图2，当点P在AD上时，过E作EQ⊥AB于Q，

∵PD=3，AD=4，

∴AP=1，

∴PB=

∵EF垂直平分PB，

∴∠1=∠2，

∵∠A=∠EQF，

∴△ABP∽△EFQ，

∴，即

解得EF=

综上所述：EF长为或

故答案为：或