��Ŀ����
����Ŀ��A���з���200t��B���з���300t����Ҫ����Щ����ȫ������C��D���磬��A����C��D�����˷��ϵķ��÷ֱ�Ϊ20Ԫ/t��25Ԫ/t����B����C��D�����˷��ϵķ��÷ֱ�Ϊ15Ԫ/t��24Ԫ/t����C����Ҫ����240t��D����Ҫ����260t�����A�ǵ���C�����xt��
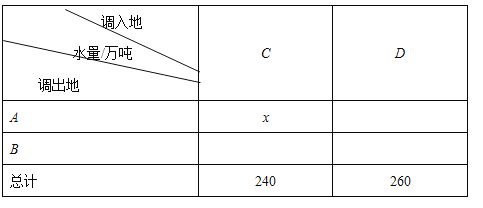
��1���������⣬��д�±���
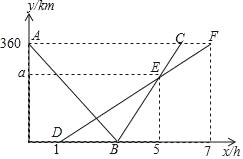
��2������˷��ϵ����˷�y����λ��Ԫ����x�ĺ�������y��x�ĺ�������ʽ��
��3������ݣ�2��������ɵ��������ܷ������ٵĵ��˷�������˵�����ɣ�
���𰸡���1��200��x��240��x��60+x����2��y=4x+10040��0��x��200������3����A������C��0�֣�����D��200�֣���B������C��240�֣�����D��60�֣���ʱ���˷����٣����˷���Сֵ��10040Ԫ��
��������
��1��A������C��ķ�����Ϊx�֣�������D��ķ�����Ϊ��200-x���֣�B������C��D��ķ������ֱ�Ϊ��240-x���ֺͣ�60+x���֣��ɴ�������ɣ�
��2�����ݣ�1���������Լ�ÿ���˷ѴӶ��ɵó�y��x��ĺ�����ϵ��
��3��x��ȡ0��200֮����κ��������ú���������������ɣ�
�⣺��1���������⣬��д�±����£�
����� ˮ��/��� ������ | C | D |
A | x | 200��x |
B | 240��x | 60+x |
�ܼ� | 240 | 260 |
�ߴ�B������C��Ϊ��240-x���֣�
���B������D��Ϊ��300-��240-x��=60+x���֣���
��2�������˷�ΪyԪ��A������C��ķ�����Ϊx�֣�������D��ķ�����Ϊ��200��x���֣�B������C��D��ķ������ֱ�Ϊ��240��x���ֺͣ�60+x���֣�
�����˷�����������Ĺ�ϵ��֪��
��ӳy��x֮��ĺ�����ϵΪ��y=20x+25��200��x��+15��240��x��+24��60+x����
����ã�y=4x+10040��
��A����200�ַ��ϣ�B����300�ַ��ϣ�C����Ҫ240�ַ��ϣ�
���A������C��ķ�����������Ϊ0�֣����Ϊ200�֣�
��0��x��200��
��y=4x+10040��0��x��200����
��3���ɽ���ʽ��֪��
��4>0��
��y��x�����������
�൱x=0ʱ��y����Сֵ10040��
��ˣ���A������C��0�֣�����D��200�֣���B������C��240�֣�����D��60�֣���ʱ���˷����٣����˷���Сֵ��10040Ԫ��

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�