题目内容
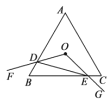
【题目】已知如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 外一点,
外一点,![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
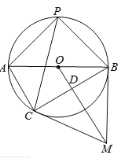
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 的长;
的长;
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)利用平行证出△BOD∽△BAC,然后列出比例式即可求出结论;
(2)连接OC,利用SAS证出△BOM≌△COM,从而证出∠OBM=∠OMB,然后根据切线的性质即可证出结论;
(3)过点A作AE⊥PC于E,根据相似三角形的判定定理证出△DOC∽△DCM,列出比例式即可求出CD,根据勾股定理求出OC,从而求出AB,然后利用锐角三角函数求出PA、AE和CE,从而求出结论.
解:(1)∵![]() ,AB=2OB
,AB=2OB
∴△BOD∽△BAC
∴![]()
∴![]() ;
;
(2)连接OC
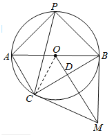
∵![]()
∴∠BOM=∠BAC
∵![]()
∴∠BOC=2∠BAC=2∠BOM
∴∠BOM=∠COM
在△BOM和△COM中
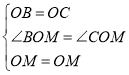
∴△BOM≌△COM
∴∠OBM=∠OMB
∵![]() 与
与![]() 相切于点
相切于点![]() ,
,
∴∠OBM=90°,
∴∠OMB=90°
∴![]() 是
是![]() 的切线;
的切线;
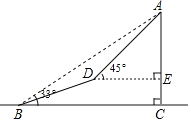
(3)过点A作AE⊥PC于E
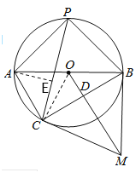
∵AB为直径
∴∠ACB=∠APB=90°
∵![]() ,
,
∴∠CDM=∠ACB =90°,∠ODC=90°
∵∠OCM=90°,
∴∠DOC+∠OCD=90°,∠DCM+∠OCD=90°
∴∠DOC=∠DCM
∴△DOC∽△DCM
∴![]()
即![]()
解得:CD=12
根据勾股定理可得OC=![]()
∴AB=2OC=30
由(1)知AC=2OD=18
∵![]()
∴△PAB为等腰直角三角形,
∴∠PAB=∠PBA=45°,
∴∠ACP=∠PBA=45°,PA=AB·sin∠PBA=![]()
∴△ACE为等腰直角三角形
∴∠ECA=45°
∴CE=AE=AC·sin∠ECA=![]()
根据勾股定理PE=![]()
∴PC=PE+CE=![]()

练习册系列答案
相关题目