题目内容
 如图,直线a∥b,则∠ACB的度数为
如图,直线a∥b,则∠ACB的度数为
- A.40°
- B.62°
- C.78°
- D.102°
C
分析:过C作a、b的平行线CD,根据平行线的内错角相等,可求得∠ACD、∠BCD的度数,进而可得∠ACB的度数.
解答: 解:过C作CD∥a,则CD∥b;
解:过C作CD∥a,则CD∥b;
∴∠DCA=28°,∠DCB=50°(两直线平行,内错角相等),
∴∠ACB=∠DCA+∠DCB=78°,
故选C.
点评:此题主要利用平行线的性质求解,正确地作出辅助线是解题的关键.
分析:过C作a、b的平行线CD,根据平行线的内错角相等,可求得∠ACD、∠BCD的度数,进而可得∠ACB的度数.
解答:
 解:过C作CD∥a,则CD∥b;
解:过C作CD∥a,则CD∥b;∴∠DCA=28°,∠DCB=50°(两直线平行,内错角相等),
∴∠ACB=∠DCA+∠DCB=78°,
故选C.
点评:此题主要利用平行线的性质求解,正确地作出辅助线是解题的关键.

练习册系列答案
相关题目
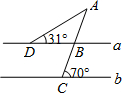 6、如图,直线a∥b,则∠A的度数是( )
6、如图,直线a∥b,则∠A的度数是( )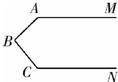 24、如图,直线AM∥CN,则∠A+∠B+∠C=
24、如图,直线AM∥CN,则∠A+∠B+∠C=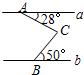 4、如图,直线a∥b,则∠ACB的度数为( )
4、如图,直线a∥b,则∠ACB的度数为( )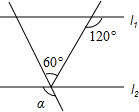 如图,直线l1∥l2,则∠а为( )
如图,直线l1∥l2,则∠а为( )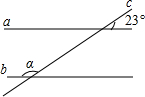 (2012•乌鲁木齐)如图,直线a∥b,则∠α=
(2012•乌鲁木齐)如图,直线a∥b,则∠α=