题目内容
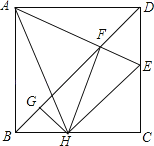
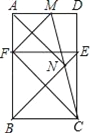
【题目】已知:矩形ABCD内一点N,△ANB为等腰直角三角形,连结BN、CN并延长分别交DC,AD于点E,M,在AB上截取BF=EC,连接MF.
(1)求证:四边形FBCE为正方形;
(2)求证:MN=NC;
(3)若S△FMC:S正方形FBCE=2:3,求BN:MD的值.
【答案】(1)证明见解析;(2)证明见解析;(3)BN:MD=![]() .
.
【解析】试题分析:(1)先证明四边形![]() 为矩形,再利用
为矩形,再利用![]() 为等腰直角三角形,证明
为等腰直角三角形,证明![]() 为等腰直角三角形,则
为等腰直角三角形,则![]() ,所以四边形
,所以四边形![]() 为正方形;
为正方形;
(2)作辅助线,构建全等三角形,证明![]() ≌
≌![]() ,得
,得![]() ,再利用平行线分线段成比例定理可得
,再利用平行线分线段成比例定理可得![]() 则
则![]()
(3)设![]() 表示出
表示出![]() 和S正方形FBCE,并根据S△FMC:S正方形FBCE=2:3,依次计算出
和S正方形FBCE,并根据S△FMC:S正方形FBCE=2:3,依次计算出![]() 的长,最后得结论.
的长,最后得结论.
试题解析:(1)如图1,∵四边形ABCD为矩形,
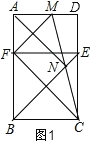
∴AB∥CD,![]()
∴BF∥EC,
∵BF=EC,
∴四边形FBCE为矩形,
∵△ANB为等腰直角三角形,
![]()
![]()
∴△BEC为等腰直角三角形,
∴BC=CE,
∴四边形FBCE为正方形;
(2)如图2,过N作GH⊥BC,交BC于H,AD于G,则GH⊥AD,
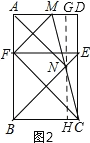
![]()
∴△BHN≌△AGN,
∴NG=NH,
∵AD∥BC,
∴![]()
∴MN=NC;
(3)如图2,设BF=1,则S正方形FBCE=1,![]() ,
,
∵FO=OC,MN=NC,
∴ON∥FM,
![]()
![]()
由于S△FMC:S正方形FBCE=2:3,
即![]()
![]()
![]()
![]()
∴△AFM是等腰直角三角形,
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目