��Ŀ����
����Ŀ���µ�Ƽ�����˾��160��Ԫ����Ϊ�²�Ʒ���з����ã��ɹ����Ƴ���һ���г�����ĵ��Ӳ�Ʒ�����ڵ���Ͷ���������������ۣ���֪�������ֵ��Ӳ�Ʒ�ijɱ�Ϊ4Ԫ/���������۹����з��֣�ÿ�����������y������������ۼ۸�x��Ԫ/�����Ĺ�ϵ��ͼ��ʾ������ABΪ����������ͼ���һ���֣�BCΪһ�κ���ͼ���һ���֣��蹫˾�������ֵ��Ӳ�Ʒ��������Ϊs����Ԫ������ע������һ��ӯ������ӯ����������һ�������������һ���������������һ��ijɱ�����
��1�������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2�������һ�����ֵ��Ӳ�Ʒ��������s����Ԫ����x��Ԫ/����֮��ĺ�����ϵʽ���������һ������������ֵ��
��3�����蹫˾�����ֵ��Ӳ�Ʒ��һ��ǡ�ð�������s����Ԫ��ȡ�����ֵʱ�������ۣ��ָ��ݵ�һ���ӯ������������ڶ��꽫���ֵ��Ӳ�Ʒÿ�������ۼ۸�x��Ԫ������8Ԫ���ϣ�x��8�������ڶ������������103��Ԫʱ������������s����Ԫ�������ۼ۸�x��Ԫ/�����ĺ���ʾ��ͼ�������ۼ۸�x��Ԫ/������ȡֵ��Χ��

���𰸡���1��y= ����2����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��ͼ����������11��x��21ʱ���ڶ����������s������103��Ԫ��
����2����ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ����3��ͼ����������11��x��21ʱ���ڶ����������s������103��Ԫ��
�������������������1�����ݴ���ϵ�������������y���������x��Ԫ/����֮��ĺ�����ϵʽ��
��2������������������ۣ���x=8ʱ��zmax=-80����x=16ʱ��zmax=-16������-16>-80���ɵõ�ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ-16��Ԫ��
��3�����ݵڶ����������z=��x-4����-x+28��-16=-x2+32x-128����z=103���ɵ÷���103=-x2+32x-128�����x1=11��x2=21��Ȼ����ƽ��ֱ������ϵ�У�����z��x�ĺ���ͼ����ͼ�ɵó����ۼ۸�x��Ԫ/������ȡֵ��Χ��
�����������1����4��x��8ʱ����y=![]() ����A��4��40�������k=4��40=160��
����A��4��40�������k=4��40=160��
��y��x֮��ĺ�����ϵʽΪy=![]() ��
��
��8��x��28ʱ����y=k'x+b����B��8��20����C��28��0������,
��: ![]() �����
�����![]() ��
��
��y��x֮��ĺ�����ϵʽΪy=��x+28��
����������y=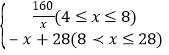 ��
��
��2����4��x��8ʱ��s=��x��4��y��160=��x��4��![]() ��160=��
��160=��![]() ��
��
�ߵ�4��x��8ʱ��s����x�����������
�൱x=8ʱ��smax=��![]() =��80��
=��80��
��8��x��28ʱ��s=��x��4��y��160=��x��4������x+28����160=����x��16��2��16��
�൱x=16ʱ��smax=��16��
����16����80��
�൱ÿ�������ۼ۸�Ϊ16Ԫʱ����һ������������ֵΪ��16��Ԫ��
��3���ߵ�һ���������Ϊ��16��Ԫ��
��16��ԪӦ��Ϊ�ڶ���ijɱ���
�֡�x��8��
��ڶ����������s=��x��4������x+28����16=��x2+32x��128��
��s=103����103=��x2+32x��128��
���x1=11��x2=21��
��ƽ��ֱ������ϵ�У�����s��x�ĺ���ʾ��ͼ�ɵã�
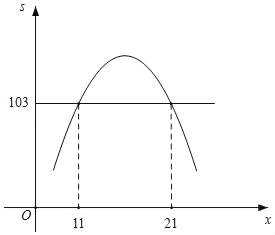
�۲�ʾ��ͼ��֪����s��103ʱ��11��x��21��
�൱11��x��21ʱ���ڶ����������s������103��Ԫ��

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�����Ŀ��2017��5��5�գ�������ɻ�C919��Բ���ɹ�.C919���й�������¹����ʺ�������������֪ʶ��Ȩ�ĸ������÷ɻ�����2008�꿪ʼ���ƣ���China������ĸ����һ����9����Ԣ�����쳤�ؾã���19�����������й������Ϳͻ�����ؿ���Ϊ190������ֹ2018��2�µף�C919���Ϳͻ��Ĺ������û��ﵽ28�ң�������������800�ܣ���1������20�ҿͻ��Ķ������
��1��
�ͻ� | �������ܣ� | �ͻ� | �������ܣ� |
�й����ʺ��� | 20 | ����������������˾ | 45 |
�й��������� | 20 | ƽ��������������˾ | 50 |
�й��Ϸ����� | 20 | ����������������˾ | 30 |
���Ϻ��� | 20 | �й��ɻ���������˾ | 20 |
�Ĵ����� | 15 | ������������˽������˾ | 20 |
�ӱ����� | 20 | ũ��������������˾ | 45 |
�Ҹ����� | 20 | ���Ž������ɷ�����˾ | 50 |
����������������˾ | 15 | ����������������˾ | 30 |
����ͨ������˾ | 20 | ��ҵ��������˾ | 20 |
̩�����к��� | 10 | �¹����ʺ��չ�˾ | 7 |
���ݱ�1���ṩ�����ݲ�ȫ��2
��2:
�������ܣ� | 7 | 10 | 15 | 20 | 30 | 45 | 50 |
�������ܣ� | 1 | 1 | 2 | 2 | 2 |
��20�����ݵ���λ��Ϊ ������Ϊ ��
����Ŀ��̽���⣮
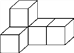
�����Ӱڳɵ���T������ͼ��ͼ��ʾ��

��1�������
ͼ����� | �� | �� | �� | �� | �� | �� |
ÿ��ͼ�������Ӹ��� | 5 | 8 | �� |
��2��д����n����T������ͼ�������ӵĸ������ú�n�Ĵ���ʽ��ʾ����
��3����20����T������ͼ���������Ӷ��ٸ���
��4������ǰ20����T������ͼ�������ӵ��ܸ���������ʾ��������˼���������⣺��1��ͼ�����20��ͼ���й��ж��ٸ����ӣ���2��ͼ�����19��ͼ���й��ж��ٸ����ӣ���3��ͼ�����18��ͼ���أ���