题目内容
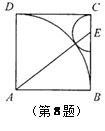
(2011•成都)已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(1)求证:AE=CK;
(2)如果AB=a,AD=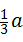 (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.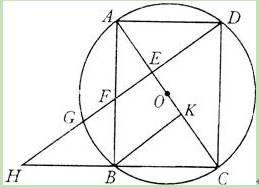
(1)求证:AE=CK;
(2)如果AB=a,AD=
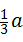 (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.

(1)证明:∵四边形据ABCD是矩形,
∴AD=BC,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△ADE,
∴AE=CK;
(2)∵AB=a,AD=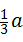 =BC,
=BC,
∴AC=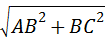 =
=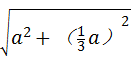 =
=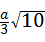
∵BK⊥AC,
∴△BKC∽△ABC,
∴ =
=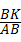 ,
,
∴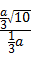 =
=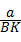 ,
,
∴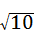 BK=a,
BK=a,
∴BK=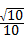 a.
a.
(3)连接OF,
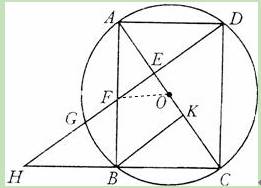
∵ABCD为矩形,
∴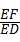 =
=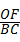 ,
,
∴EF=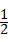 ED=
ED=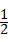 ×6=3,
×6=3,
∵F是EG的中点,
∴GF=EF=3,
∵△AFD≌△HBF,
∴HF=FE=3+6=9,
∴GH=6,
∵DH∥KB,ABCD为矩形,
∴AE2=EF•ED=3×6=18,
∴AE=3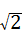 ,
,
∵△AED∽△HEC,
∴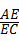 =
=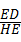 =
=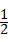 ,
,
∴AE=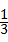 AC,
AC,
∴AC=9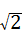 ,
,
则AO=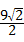 .
.
∴AD=BC,
∵BK⊥AC,DH∥KB,
∴∠BKC=∠AED=90°,
∴△BKC≌△ADE,
∴AE=CK;
(2)∵AB=a,AD=
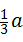 =BC,
=BC,∴AC=
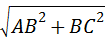 =
=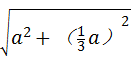 =
=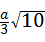
∵BK⊥AC,
∴△BKC∽△ABC,
∴
 =
=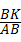 ,
,∴
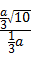 =
=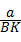 ,
,∴
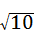 BK=a,
BK=a,∴BK=
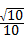 a.
a.(3)连接OF,

∵ABCD为矩形,
∴
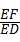 =
=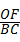 ,
,∴EF=
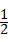 ED=
ED=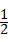 ×6=3,
×6=3,∵F是EG的中点,
∴GF=EF=3,
∵△AFD≌△HBF,
∴HF=FE=3+6=9,
∴GH=6,
∵DH∥KB,ABCD为矩形,
∴AE2=EF•ED=3×6=18,
∴AE=3
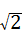 ,
,∵△AED∽△HEC,
∴
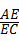 =
=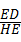 =
=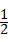 ,
,∴AE=
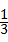 AC,
AC,∴AC=9
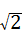 ,
,则AO=
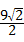 .
.略

练习册系列答案
相关题目
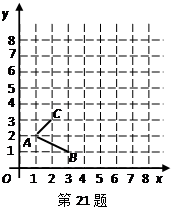
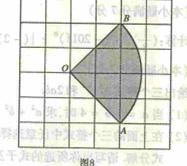

 ,则
,则 的度数为 .
的度数为 .
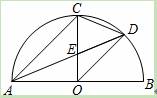
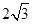 cm,则OA= cm.
cm,则OA= cm.