题目内容
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 上一点,
上一点,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明PB=PE,由ASA证明△BOQ≌△EOP;
(2)由(1)得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(3)根据三角形中位线的性质可得AE+BE=2OF+2OB=18,设AE=x,则BE=18x,在Rt△ABE中,根据勾股定理可得![]() ,BE=10,得到
,BE=10,得到![]() ,设PE=y,则AP=8y,BP=PE=y,在Rt△ABP中,根据勾股定理可得
,设PE=y,则AP=8y,BP=PE=y,在Rt△ABP中,根据勾股定理可得![]() ,解得
,解得![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得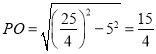 ,由PQ=2PO即可求解.
,由PQ=2PO即可求解.
解:(1)∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,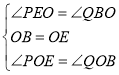 ,
,
∴![]() ,
,
(2)∵![]()
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(3)∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
设![]() ,则
,则![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
解得![]() ,
,
在![]() 中,
中,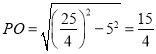 ,
,
∴![]() .
.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目