题目内容
【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
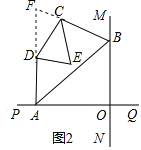
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
【答案】（1）∠AEB的大小不变135°；（2）∠CED的大小不变67.5°；（3）60°或45°．
【解析】
试题分析:（1）根据直线MN与直线PQ垂直相交于O可知∠AOB=90°，再由AE、BE分别是∠BAO和∠ABO角的平分线得出∠BAE=
∠OAB，∠ABE=∠ABO，由三角形内角和定理即可得出结论；
（2）延长AD、BC交于点F，根据直线MN与直线PQ垂直相交于O可得出∠AOB=90°，进而得出∠OAB+∠OBA=90°，故∠PAB+∠MBA=270°，再由AD、BC分别是∠BAP和∠ABM的角平分线，可知∠BAD=∠BAP，∠ABC=
∠ABM，由三角形内角和定理可知∠F=45°，再根据DE、CE分别是∠ADC和∠BCD的角平分线可知∠CDE+∠DCE=112.5°，进而得出结论；
（3））由∠BAO与∠BOQ的角平分线相交于E可知∠EAO=∠BAO，∠EOQ=∠BOQ，进而得出∠E的度数，由AE、AF分别是∠BAO和∠OAG的角平分线可知∠EAF=90°，在△AEF中，由一个角是另一个角的3倍分四种情况进行分类讨论．
解：（1）∠AEB的大小不变，
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∵AE、BE分别是∠BAO和∠ABO角的平分线，
∴∠BAE=∠OAB，∠ABE=∠ABO，
∴∠BAE+∠ABE=（∠OAB+∠ABO）=45°，
∴∠AEB=135°；
（2）∠CED的大小不变．
延长AD、BC交于点F．
∵直线MN与直线PQ垂直相交于O，
∴∠AOB=90°，
∴∠OAB+∠OBA=90°，
∴∠PAB+∠MBA=270°，
∵AD、BC分别是∠BAP和∠ABM的角平分线，
∴∠BAD=∠BAP，∠ABC=∠ABM，
∴∠BAD+∠ABC=（∠PAB+∠ABM）=135°，
∴∠F=45°，
∴∠FDC+∠FCD=135°，
∴∠CDA+∠DCB=225°，
∵DE、CE分别是∠ADC和∠BCD的角平分线，
∴∠CDE+∠DCE=112.5°，
∴∠E=67.5°；
（3）∵∠BAO与∠BOQ的角平分线相交于E，
∴∠EAO=∠BAO，∠EOQ=∠BOQ，
∴∠E=∠EOQ﹣∠EAO=（∠BOQ﹣∠BAO）=∠ABO，
∵AE、AF分别是∠BAO和∠OAG的角平分线，
∴∠EAF=90°．
在△AEF中，
∵有一个角是另一个角的3倍，故有：
①∠EAF=3∠E，∠E=30°，∠ABO=60°；
②∠EAF=3∠F，∠E=60°，∠ABO=120°；
③∠F=3∠E，∠E=22.5°，∠ABO=45°；
④∠E=3∠F，∠E=67.5°，∠ABO=135°．
∴∠ABO为60°或45°．
