题目内容
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.

【答案】(1)小颖参加比赛的概率为:![]() ;(2)游戏不公平;可改为:若两个数字之和小于5,则小颖去参赛;否则,小亮去参赛.
;(2)游戏不公平;可改为:若两个数字之和小于5,则小颖去参赛;否则,小亮去参赛.
【解析】
试题分析:(1)首先根据题意画出树状图,由树状图求得所有等可能的结果与两指针所指数字之和和小于4的情况,则可求得小颖参加比赛的概率;
(2)根据小颖获胜与小亮获胜的概率,比较概率是否相等,即可判定游戏是否公平;使游戏公平,只要概率相等即可.
解:(1)画树状图得:
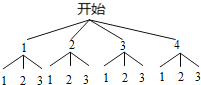
∵共有12种等可能的结果,所指数字之和小于4的有3种情况,
∴P(和小于4)=![]() =
=![]() ,
,
∴小颖参加比赛的概率为:![]() ;
;
(2)不公平,
∵P(小颖)=![]() ,
,
P(小亮)=![]() .
.
∴P(和小于4)≠P(和大于等于4),
∴游戏不公平;
可改为:若两个数字之和小于5,则小颖去参赛;否则,小亮去参赛.

练习册系列答案
相关题目