题目内容
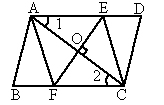
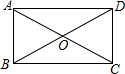
已知: ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD, A、C两点恰好都落在O点处,且四边形DEBF为菱形(如图).
⑴求证:四边形ABCD是矩形;
⑵在四边形ABCD中,求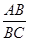 的值.
的值.
(1)证明:连结OE 
∵四边形ABCD是平行四边形,
∴DO=OB,
∵四边形DEBF是菱形,
∴DE=BE,
∴EO⊥BD
∴∠DOE= 90°
即∠DAE= 90°
又四边形ABCD是平行四边形,
∴四边形ABCD是矩形
(2)解:∵四边形DEBF是菱形
∴∠FDB=∠EDB
又由题意知∠EDB=∠EDA
由(1)知四边形ABCD是矩形
∴∠ADF=90°,即∠FDB+∠EDB+∠ADE=90°
则∠ADB= 60°
∴在Rt△ADB中,有AD∶AB=1∶
即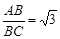
解析

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 已知?ABCD的对角∠BAD和∠BCD互补.
已知?ABCD的对角∠BAD和∠BCD互补. 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是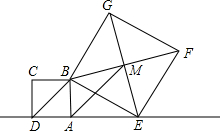 如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形.
如图,已知正方形ABCD的边长为1,点E是射线DA一动点(DE>1),连结BE,以BE为边在BE上方作正方形BEFG,设M为正方形BEFG的中心,如果定义:只有一组对角是直角的四边形叫做损矩形. ABCD的对角AC的垂直平分线与边AD、BC分别交于E、F(如图).
ABCD的对角AC的垂直平分线与边AD、BC分别交于E、F(如图).