题目内容
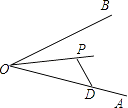
【题目】如图,AD为△ABC的高,BE为△ABC的角平分线,若∠EBA=34°,∠AEB=72°.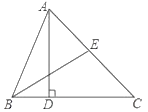
(1)求∠CAD和∠BAD的度数;
(2)若点F为线段BC上任意一点,当△EFC为直角三角形时,试求∠BEF的度数.
【答案】
(1)解:∵BE为△ABC的角平分线,
∴∠CBE=∠EBA=34°,
∵∠AEB=∠CBE+∠C,
∴∠C=72°﹣34°=38°,
∵AD为△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=52°,
∠BAD=90°-∠ABD=90°-68°=22°
(2)解:当∠EFC=90°时,∠BEF=90°﹣∠CBE=56°,
当∠FEC=90°时,∠BEF=180°-72°﹣90°=18°
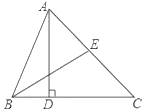
【解析】(1)由BE为∠ABC的平分线,得出∠BAD=22°,再求出∠C,得出∠CAD=52°,即可得出结论;
(2)分两种情况:①当∠EFC=90°时;②当∠FEC=90°时;由角的互余关系和三角形的外角性质即可求出∠BEF的度数.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握垂线的性质(垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短)的相关知识才是答题的关键.

练习册系列答案
相关题目