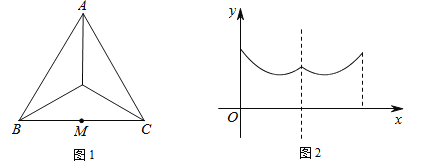��Ŀ����
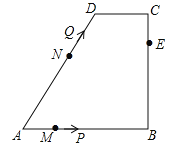
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����B=90�㣬AB=AD=5��BC=4��M��N��E�ֱ���AB��AD��CB�ϵĵ㣬AM=CE=1��AN=3����P�ӵ�M��������ÿ��1����λ���ȵ��ٶ�������MB��BE���E�˶���ͬʱ��Q�ӵ�N����������ͬ���ٶ�������ND��DC��CE���E�˶���������һ���㵽�����һ����Ҳֹͣ�˶�������APQ�����ΪS���˶�ʱ��Ϊt�룬��S��t������ϵ�Ĵ���ͼ��Ϊ�� ��
A��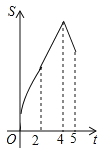 B��
B��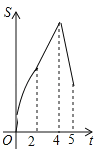 C��
C��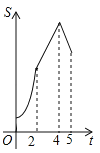 D��
D��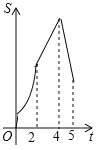
���𰸡�D��
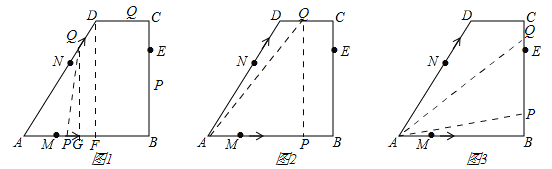
����������AD=5��AN=3����DN=2����ͼ1������D��DF��AB����DF=BC=4����RT��ADF�У�AD=5��DF=4�����ݹ��ɶ����ã�AF=![]() =3����BF=CD=2������Q����Dʱ����2s������PҲ�˶�2s����AP=3����QP��AB����ֻ�����������
=3����BF=CD=2������Q����Dʱ����2s������PҲ�˶�2s����AP=3����QP��AB����ֻ�����������
�ٵ�0��t��2ʱ����ͼ1����Q��QG��AB������D��DF��AB��QG��DF����![]() ��������ã�NQ=t��MP=t����AM=1��AN=3����AQ=t+3����
��������ã�NQ=t��MP=t����AM=1��AN=3����AQ=t+3����![]() ����QG=
����QG=![]() ��t+3������AP=t+1����S=S��APQ=
��t+3������AP=t+1����S=S��APQ=![]() AP��QG=
AP��QG=![]() ����t+1����
����t+1����![]() ��t+3��=
��t+3��=![]() ����t=2ʱ��S=6��
����t=2ʱ��S=6��
�ڵ�2��t��4ʱ����ͼ2����AP=AM+t=1+t����S=S��APQ=![]() AP��BC=
AP��BC=![]() ��1+t����4=2��t+1��=2t+2����t=4ʱ��S=8��
��1+t����4=2��t+1��=2t+2����t=4ʱ��S=8��
�۵�4��t��5ʱ����ͼ3���������CQ=t��4��PB=t+AM��AB=t+1��5=t��4����PQ=BC��CQ��PB=4����t��4������t��4��=12��2t����S=S��APQ=![]() PQ��AB=
PQ��AB=![]() ����12��2t����5=��5t+50����t=5ʱ��S=5��
����12��2t����5=��5t+50����t=5ʱ��S=5��
��S��t�ĺ�����ϵʽ�ֱ��Ǣ�S=S��APQ=![]() ����t=2ʱ��S=6����S=S��APQ=2t+2����t=4ʱ��S=8������S=S��APQ=��5t+50����t=5ʱ��S=5���ۺ��������������D��ȷ����ѡD��
����t=2ʱ��S=6����S=S��APQ=2t+2����t=4ʱ��S=8������S=S��APQ=��5t+50����t=5ʱ��S=5���ۺ��������������D��ȷ����ѡD��

 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�