题目内容
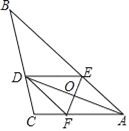
【题目】如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF.
(1)判断四边形AFDE是什么四边形?请说明理由;
(2)若BD=8,CD=3,AE=4,求CF的长.
【答案】(1)四边形AEDF是菱形,理由见解析;(2)CF= ![]() .
.
【解析】试题分析:(1)由于O是AD的中点,且EF⊥AD,所以AE=DE,AF=DF,由于AD平分∠BAC,所以∠EAO=∠FAO=90°,从易证AE=AF=DF=DE,所以四边形AEDF是菱形.
(2)由DE∥AC可知△BDE∽△BCA,从而可知![]() ,代入数据即可求出AC的长度,从而可知CF的长度.
,代入数据即可求出AC的长度,从而可知CF的长度.
试题解析:(1)四边形AEDF是菱形,理由如下:
∵O是AD的中点,且EF⊥AD,
∴AE=DE,AF=DF,
∵AD平分∠BAC,
∴∠EAO=∠FAO,
∵∠EOA=∠FOA=90°,
∴∠OEA=∠OFA,
∴AE=AF,
∴AE=AF=DF=DE,
∴四边形AEDF是菱形.
(2)∵四边形AEDF是菱形,
∴DE∥AC.
∴△BDE∽△BCA.
∴![]() ,
,
∴![]()
∴AC=![]()
∴CF=AC﹣CF=![]() .
.


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目