题目内容
【题目】如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.
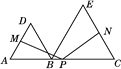
(1)求证:PM=PN;
(2)求∠MPN的度数.
【答案】(1)证明见解析;(2) ∠MPN=120°.
【解析】试题分析:(1)连接CD、AE,由△ABD和△BCE是等边三角形得AB=DB,BE=BC,∠ABD=∠CBE=60°,易证△ABE≌△DBC,得AE=DC,再由三角形中位线的性质可证PM=PN;
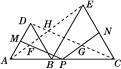
(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H,易证四边形PFHG为平行四边形,故∠MPN=120°.
试题解析:(1)如图,连接CD,AE.由三角形中位线定理可得PM=![]() CD,PN=
CD,PN=![]() AE,∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°,∴∠ABE=∠DBC.
AE,∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°,∴∠ABE=∠DBC.
∴△ABE≌△DBC,∴AE=DC.∴PM=PN.
(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H.由(1)知△ABE≌△DBC,∴∠BAE=∠BDC.
∴∠AHD=∠ABD=60°,∴∠FHG=120°.
易证四边形PFHG为平行四边形,∴∠MPN=120°.

练习册系列答案
相关题目
【题目】某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
求A、B两种型号的电风扇的销售单价.