题目内容
已知a、b、c为△ABC的三条边,且满足a2+b2+c2=10a+24b+26c-338.
(1)试判断三角形的形状;
(2)求三角形最长边上的高.
解:(1)∵a2+b2+c2=10a+24b+26c-338
∴a2-10a+b2-24b+c2-26c+338=0
a2-10a+25+b2-24b+144+c2-26c+169=0
(a-5)2+(b-12)2+(c-13)2=0
∴(a-5)2=0,(b-12)2=0,(c-13)2=0
∴a=5,b=12,c=13
∴a2+b2=c2=169
∴△ABC是直角三角形;
(2)△ABC最长边为c,
设c上的高为h.
S△ABC=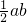
= ×5×12
×5×12
=30,
又∵S△ABC= =30
=30 =30,
=30,
∴h= .
.
分析:(1)先将式子进行化简,配方成完全平方的形式,求得a,b,c,根据勾股定理的逆定理进行判断即可;
(2)根据(1)求出三角形的面积,再由最长边乘以最长边上的高除以2也等于这个三角形的面积,求出最长边上的高.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可;直角三角形有两种求面积的方法.
∴a2-10a+b2-24b+c2-26c+338=0
a2-10a+25+b2-24b+144+c2-26c+169=0
(a-5)2+(b-12)2+(c-13)2=0
∴(a-5)2=0,(b-12)2=0,(c-13)2=0
∴a=5,b=12,c=13
∴a2+b2=c2=169
∴△ABC是直角三角形;
(2)△ABC最长边为c,
设c上的高为h.
S△ABC=
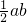
=
 ×5×12
×5×12=30,
又∵S△ABC=
 =30
=30 =30,
=30,∴h=
 .
.分析:(1)先将式子进行化简,配方成完全平方的形式,求得a,b,c,根据勾股定理的逆定理进行判断即可;
(2)根据(1)求出三角形的面积,再由最长边乘以最长边上的高除以2也等于这个三角形的面积,求出最长边上的高.
点评:本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可;直角三角形有两种求面积的方法.

练习册系列答案
相关题目


 (1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为
(1997•贵阳)已知:如图,CD为⊙O的直径,CD⊥AB,M为垂足,DM=2cm,弦AB=8cm,则⊙O的半径为 P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.