题目内容
如图,在直角坐标系中,点C( ,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒
,0),点D(0,1),CD的中垂线交CD于点E,交y轴于点B,点P从点C出发沿CO方向以每秒 个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
个单位的速度运动,同时点Q从原点O出发沿OD方向以每秒1个单位的速度向点D运动,当点Q到达点D时,点P,Q同时停止运动,设运动的时间为秒。
(1)求出点B的坐标。
(2)当为何值时,△POQ与△COD相似?
(3)当点P在x轴负半轴上时,记四边形PBEQ的面积为S,求S关于的函数关系式,并写出自变量的取值范围;
(4)在点P、Q的运动过程中,将△POQ绕点O旋转1800,点P的对应点P′,点Q的对应点Q′,当线段P′Q′与线段BE有公共点时,抛物线 经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出:
经过P′Q′的中点,此时的抛物线与x轴正半轴交于点M。由已知,直接写出:
① 的取值范围为 ;
的取值范围为 ;
②点M移动的平均速度是 。
(1)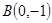 ;(2)
;(2) (3)y=
(3)y=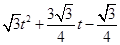 (
(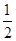 <
<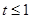 );(4)①
);(4)①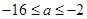 ;②点M移动的平均速度为每秒
;②点M移动的平均速度为每秒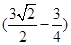 个单位.
个单位.
解析试题分析:(1)由题意得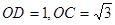 ,由勾股定理得
,由勾股定理得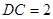 ,证得
,证得 ≌
≌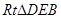 ,再结合垂直平分线的性质求解即可;
,再结合垂直平分线的性质求解即可;
(2)分①当点P在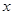 轴的正半轴上时,②当点P在
轴的正半轴上时,②当点P在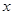 轴的负半轴上时,根据相似三角形的性质求解;
轴的负半轴上时,根据相似三角形的性质求解;
(3)由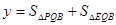 ,根据三角形的面积公式求解即可;
,根据三角形的面积公式求解即可;
(4)当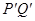 与
与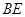 有公共点时,初始位置点P′与点A重合由已知得,
有公共点时,初始位置点P′与点A重合由已知得,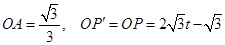 ,即可求得
,即可求得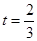 ,根据终止位置点P′与点C重合,点Q′与点B重合,这时
,根据终止位置点P′与点C重合,点Q′与点B重合,这时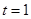 ,从而可得t的范围,设
,从而可得t的范围,设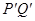 的中点为F,当
的中点为F,当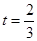 时,
时,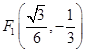 ,把
,把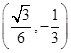 代入
代入 得:
得: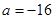 ,当
,当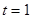 时
时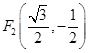 ,把
,把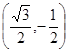 代入
代入 ,得:
,得: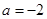 ,即可得到
,即可得到 的取值范围,则可得初始位置的抛物线为
的取值范围,则可得初始位置的抛物线为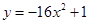 ,此时
,此时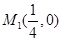 ,终止位置的抛物线为
,终止位置的抛物线为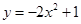 ,此时
,此时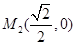 ,则
,则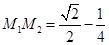 ,再根据移动的时间为
,再根据移动的时间为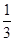 秒即可求得结果.
秒即可求得结果.
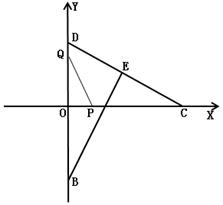
(1)由题意得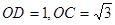 ,由勾股定理得:
,由勾股定理得: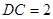
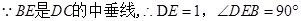
在 与
与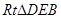 中
中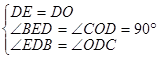
∴ ≌
≌ 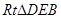
∴BD=DC=2,
∴BO=1
∴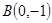 ;
;
(2)①当点P在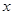 轴的正半轴上时,
轴的正半轴上时,
由已知得,CP=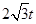 ,OP=CO-CP=
,OP=CO-CP=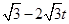 ,
,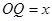
由题意得: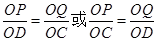
即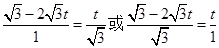 ,解得
,解得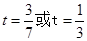 ;
;
②当点P在 轴的负半轴上时
轴的负半轴上时
由题意得: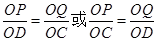
即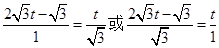 ,解得
,解得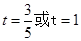
综上所述:当 △POQ与△COD相似;
△POQ与△COD相似;
(3)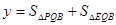
 =
=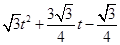 (
(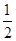 <
<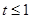 );
);
(4)当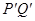 与
与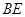 有公共点时,初始位置点P′与点A重合
有公共点时,初始位置点P′与点A重合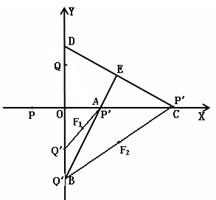
由已知得,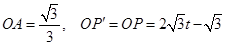
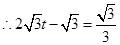 ,解得
,解得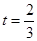
终止位置点P′与点C重合,点Q′与点B重合,这时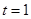
∴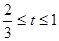
设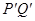 的中点为F,当
的中点为F,当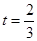 时,
时,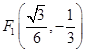
把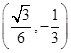 代入
代入 得:
得: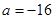
当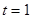 时
时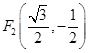


 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: