题目内容
【题目】问题情境：在综合与实践课上，同学们以“已知三角形三边的长度，求三角形面积”为主题开展数学活动，小颖想到借助正方形网格解决问题．图 1，图 2 都是 8×8 的正方形网格，每个小正方形的边长均为 1，每个小正方形的顶点称为格点．
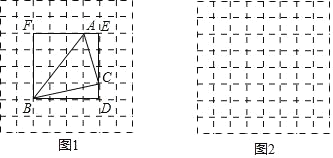
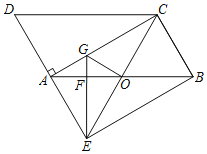
操作发现：小颖在图 1 中画出△ABC，其顶点 A，B，C 都是格点，同时构造正方形 BDEF， 使它的顶点都在格点上，且它的边 DE，EF 分别经过点 C，A，她借助此图求出了△ABC 的面积．
（1）在图 1 中，小颖所画的△ABC 的三边长分别是 AB＝ ，BC＝ ，AC
＝ ；△ABC 的面积为 ． 解决问题：
（2）已知△ABC 中，AB＝
，BC＝2 
，AC＝5 
，请你根据小颖的思路，在图 2的正方形网格中画出△ABC，并直接写出△ABC 的面积．
【答案】（1）
；（2）图见解析，5
【解析】
根据勾股定理、矩形的面积公式、三角形面积公式计算．
解：（1）AB＝
＝5，BC＝
＝
，AC＝
＝
，
△ABC 的面积为：4×4﹣
×3×4-×1×4﹣×3×1＝ 
，
故答案为：5; ;;;
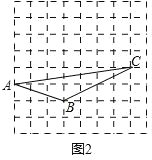
（2）△ABC 的面积：7×2﹣×3×1﹣ ×4×2﹣ ×7×1＝5．
名校课堂系列答案
【题目】为积极响应“弘扬传统文化”的号召，某学校组织全校1200名学生进行经典诗词诵读活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取40名学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图如图所示．
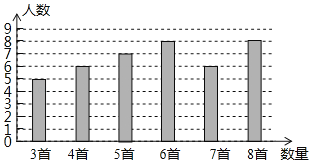
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表如下：
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
（1）活动启动之初学生“一周诗词诵背数量”的中位数为_____________，平均数为___________；
（2）选择适当的统计量，至少从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．
