题目内容
【题目】综合题。
（1）计算：（ 
﹣1）0+2sin30°﹣（ 
）﹣1+|﹣2017|；
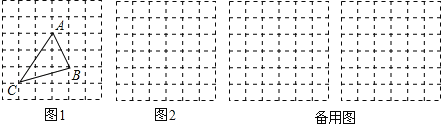
（2）如图，在△ABC中，已知∠ABC=30°，将△ABC绕点B逆时针旋转50°后得到△A1BC1 ， 若∠A=100°，求证：A1C1∥BC．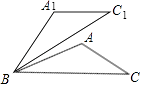 
【答案】
（1）解：原式=1+2× 
﹣2+2017
=1+1﹣2+2017
=2017
（2）证明：在△ABC中，∵∠ABC=30°，∠A=100°，
∴∠C=180°﹣∠A﹣∠ABC=50°．
∵将△ABC绕点B逆时针旋转50°后得到△A1BC1，
∴∠C1=∠C=50°，∠C1BC=50°．
∴∠C1=∠C1BC，
∴A1C1∥BC．
【解析】（1）原式利用零指数幂的意义、特殊角的三角函数值、负整数指数幂的意义以及绝对值的代数意义计算即可得到结果；（2）先在△ABC中利用三角形内角和定理求出∠C=50°，再根据旋转的性质求出∠C1=∠C=50°，∠C1BC=50°．等量代换得出∠C1=∠C1BC，根据平行线的判定即可证明A1C1∥BC．
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)才能正确解答此题．
练习册系列答案
相关题目
