题目内容
如图,在四边形ABCD中,M、N分别是CD、BC的中点, 且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADC度数为( ) .

A、45° B、47° C、49° D、51°

A、45° B、47° C、49° D、51°
C
试题分析:首先要求出∠3,∠4的度数,然后连接AC,利用角与角的和差关系求得∠ADC的度数.
∵AM⊥CD,AN⊥BC,∠MAN=74°,∠DBC=41°即∠4=41°,
∴四边形AMCN是圆内接四边形,
∴∠MAN+∠BCD=180°,
∴∠BCD=180°-∠MAN=180°-74°=106°
∴∠3=180-∠2-∠BCD=180°-41°-106°=33°,
连接AC

∵M、N分别是CD、BC的中点,且AM⊥CD,AN⊥BC,
∴AB=AC=AD,∠1=∠2,
∠1+∠4=∠ACB---①,
∠2+∠3=∠ACD----②
∠ACB+∠ACD=∠NCM=106°---③
由①②③得∠1+∠2+∠3+∠4=106°
∵∠1=∠2,∠4=41°,∠3=33°,
代入得:∠2=16°,
故∠ADC=∠2+∠3=16°+33°=49°.
故选C.
点评:作出辅助线后利用线段垂直平分线的性质,四边形及三角形的内角和定理解答是解答本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目

 ,则平行四边形ABCD的面积为
,则平行四边形ABCD的面积为

 )
)
 ,
, 与
与 的平分线交于点
的平分线交于点 .
.
 = (度);
= (度); 上.
上. 
 中,点
中,点 、
、 分别在
分别在 、
、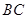 上,
上, 为等腰直角三角形,
为等腰直角三角形, 求
求