题目内容
如图,抛物线y1=- x2+3与x轴交于A、B两点,与直线y2=-
x2+3与x轴交于A、B两点,与直线y2=- x+b相交于B、C两点.
x+b相交于B、C两点.
(1)求直线BC的解析式和点C的坐标;
(2)若对于相同的x,两个函数的函数值满足y1≥y2,则自变量x的取值范围是 .
(1)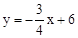 ,
,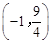 ;
;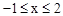 .
.
解析试题分析:(1)令y=0求解得到点B的坐标,把点B的坐标代入直线解析式求出b的值,再与直线联立求解得到点C的坐标;(2)根据函数图象找出抛物线在直线上方部分的x的取值范围:由图可知,y1≥y2时,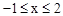 .
.
试题解析:(1)令y=0,则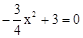 ,解得x1=-2,x2=2,∴点B的坐标为(2,0),
,解得x1=-2,x2=2,∴点B的坐标为(2,0),
∴ ,解得b=6,
,解得b=6,
∴直线BC的解析式为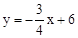 .
.
由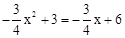 得
得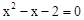 ,解得
,解得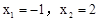 (舍去),
(舍去),
∴点C的坐标为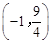 .
.
(2)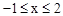 .
.
考点:1.二次函数与不等式(组);2.待定系数法求一次函数解析式;3.抛物线与x轴的交点.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 米,面积为
米,面积为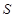 平方米.(注:
平方米.(注: 的近似值取3)
的近似值取3)

 ).
).
 上有一点M(x0,
上有一点M(x0, )位于
)位于 轴下方.
轴下方. ,0),B(
,0),B( ,0),且
,0),且 <
< .
. ?
?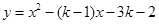 与
与 轴交于两点A
轴交于两点A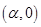 ,B
,B ,且
,且 ,求k的值.
,求k的值. (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.