题目内容
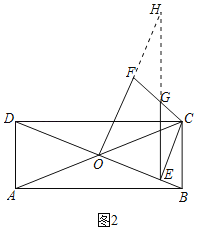
【题目】矩形ABCD的对角线相交于点O,∠COE=45°,过点C作CE⊥BD于点E,
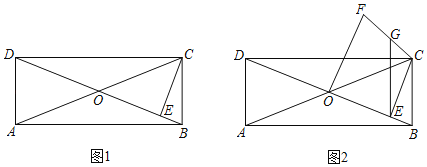
(1)如图1,若CB=1,求△CED的面积;
(2)如图2,过点O作OF⊥DB于点O,OF=OD,连接FC,点G是FC中点,连接GE,求证:DC=2GE.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)由矩形的性质得出OA=OC=OB=OD,由∠COE=45°,CE⊥BD,证出△OCE是等腰直角三角形,得出OE=CE,OC=![]() OE,设OE=CE=x,则OB=OD=OC=
OE,设OE=CE=x,则OB=OD=OC=![]() x,得出DE=(
x,得出DE=(![]() +1)x,BE=(
+1)x,BE=(![]() ﹣1)x,在Rt△BCE中,由勾股定理得:BC2=BE2+CE2=(
﹣1)x,在Rt△BCE中,由勾股定理得:BC2=BE2+CE2=(![]() ﹣1)2x2+x2=(4﹣2
﹣1)2x2+x2=(4﹣2![]() )x2=1,得出x2=
)x2=1,得出x2=![]() =
=![]() ,由三角形面积公式即可得出答案;
,由三角形面积公式即可得出答案;
(2)延长OF、EG交于点H,证明△GHF≌△GEC(AAS),得出GH=GE,FH=CE,证出ED=OH,证明△CDE≌△EHO(SAS),得出CD=EH,即可得出结论.
(1)解:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OC=OB=OD,
∵∠COE=45°,CE⊥BD,
∴△OCE是等腰直角三角形,
∴OE=CE,OC=![]() OE,
OE,
设OE=CE=x,则OB=OD=OC=![]() x,
x,
∴DE=(![]() +1)x,BE=(
+1)x,BE=(![]() ﹣1)x,
﹣1)x,
在Rt△BCE中,由勾股定理得:BC2=BE2+CE2=(![]() ﹣1)2x2+x2=(4﹣2
﹣1)2x2+x2=(4﹣2![]() )x2=1,
)x2=1,
∴x2=![]() =
=![]() ,
,
∴△CED的面积=![]() DE×CE=(
DE×CE=(![]() +1)x2=(
+1)x2=(![]() +1)×
+1)×![]() =
=![]() ;
;
(2)证明:延长OF、EG交于点H,如图所示:
∵OF⊥BD,CE⊥BD,
∴OF∥CE,∠EOH=∠CED=90°,
∴∠H=∠CEG,
∵点G是FC中点,
∴GF=GC,
在△GHF和△GEC中,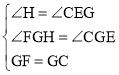 ,
,
∴△GHF≌△GEC(AAS),
∴GH=GE,FH=CE,
∴FH=OE,
∵OF=OD,
∴ED=OH,
在△CDE和△EHO中,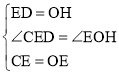 ,
,
∴△CDE≌△EHO(SAS),
∴CD=EH,
∵EH=2GE,
∴CD=2GE.