题目内容
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
【答案】
(1)解:根据描点法作函数的图象,先描点,连线即可得图象,
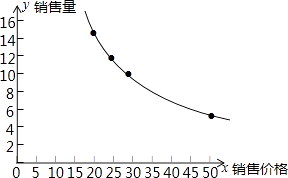
(2)解:观察表中数据可得,x与y得积为常数,判断为反比例函数,
根据数据,易得K=20×15=300,
故其解析式为 ![]() .
.
(3)解: ![]() =
= ![]()
当x≤30时,因为w随x增大而增大,
∴当x=30时,w最大=150.
【解析】(1)根据表中数据画出函数图像即可,此图像在第一象限。
(2)由表中x与y的对应值的规律,或观察图像可知此函数是反比例函数,代入x、y的对应值即可求得此函数的解析式。
(3)总利润=销售量×(售价-成本价),列函数解析式,根据售价不超过30元,即可求得结果。

练习册系列答案
相关题目