Question

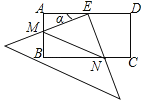
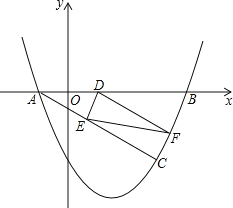
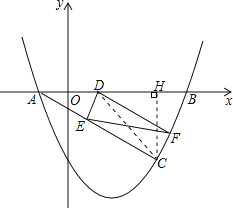
【题目】如图，已知抛物线y=﹣x﹣2图象与x轴相交于A，B两点（点A在点B的左侧）．若C（m，1﹣m）是抛物线上位于第四象限内的点，D是线段AB上的一个动点（不与A，B重合），过点D分别作DE∥BC交AC于E，DF∥AC交BC于F．

(1)、求点A和点B的坐标；

(2)、求证：四边形DECF是矩形；

(3)、连接EF，线段EF的长是否存在最小值？若存在，求出EF的最小值；若不存在，请说明理由．

Answer 1

【答案】(1)、（﹣1，0），（4，0）；(2)、证明过程见解析；(3)、2.

【解析】

试题分析：(1)、根据抛物线的解析式来求点A、B的坐标即可；(2)、欲证明四边形DECF是矩形，只需证得四边形DECF是平行四边形且有一内角为直角即可；(3)、连接CD，根据矩形DECF的对角线相等得到：EF=CD．当CD⊥AB时，CD的值最小，即EF的值最小．

试题解析：(1)、当y=0时，﹣x﹣2=0， 解方程，得 x1=﹣1，x2=4． ∵点A在点B的左侧，

∴点A、B的坐标分别是（﹣1，0），（4，0）；

(2)、把C（m，1﹣m）代入y=﹣x﹣2得：－2=1－m 解方程，得m=3或m=﹣2．

∵点C位于第四象限， ∴m＞0，1﹣m＜0，即m＞1， ∴m=﹣2舍去， ∴m=3，

∴点C的坐标为（3，﹣2）． 过点C作CH⊥AB于H，则∠AHC=∠BHC=90°．

由A（﹣1，0），B（4，0），C（3，﹣2）得到：AH=4，CH=2，BH=1，AB=5， ∴=2．

又∵∠AHC=∠CHB=90°，∴△AHC∽△CHB， ∴∠ACH=∠CBH． ∵∠CBH+∠BCH=90°，

∴∠ACH+∠BCH=90°， ∴∠ACB=90°， ∵DE∥BC，DF∥AC， ∴四边形DECF是平行四边形，

∴平行四边形DECF是矩形；

(3)、存在．理由如下： 连接CD． ∵平行四边形DECF是矩形， ∴EF=CD．

当CD⊥AB时，CD的值最小． ∵C（3，2）， ∴DC的最小值是2， ∴EF的最小值是2．