��Ŀ����
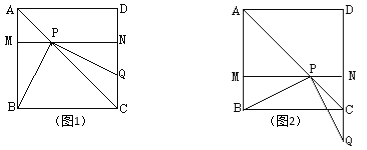
����Ŀ����������һ�����dz߷��ڱ߳�Ϊ1��������ABCD�ϣ���ʹ����ֱ�Ƕ���P�ڶԽ���AC�ϻ�����ֱ�ǵ�һ��ʼ�վ�����B����һ��������DC�ཻ�ڵ�Q����A��P�����ľ���Ϊx��
̽����
��1������Q�ڱ�CD��ʱ���߶�PQ���߶�PB֮���������Ĵ�С��ϵ����֤����۲쵽�Ľ��ۣ�
��2������Q�ڱ�CD��ʱ�����ı���PBCQ�����Ϊy����y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ����3������P���߶�AC�ϻ���ʱ����PCQ�Ƿ��ܳ�Ϊ���������Σ�������ܣ�ָ��������ʹ��PCQ��Ϊ���������εĵ�Q��λ�ã��������Ӧx��ֵ����������ܣ���˵�����ɣ�
���𰸡�(1)��PQ=PB��֤�����̼�������(2)��y=![]() (0��x��
(0��x��![]() )��(3)��x��0��1.
)��(3)��x��0��1.
��������
���������(1)������P��MN��BC���ֱ�AB��CD�ڵ�M��N�����ı���AMND���ı���BCNM���Ǿ��Σ���AMP����CNP���ǵ��������Σ��ó�NP=NC=MB���Ӷ�֤����QNP�ա�PMB���Ӷ��ó��𰸣�(2)����AP=x����M��MP��NQ��DN��![]() x��BM��PN��CN��1��
x��BM��PN��CN��1��![]() x����������ó���PBC����PCQ�������Ȼ��ó�y��x�ĺ�����ϵʽ��(3)���������������������ۣ���������Q�ڱ�DC�ϣ�������Q�ڱ�DC���ӳ����ϣ�������Q��C���غ�.
x����������ó���PBC����PCQ�������Ȼ��ó�y��x�ĺ�����ϵʽ��(3)���������������������ۣ���������Q�ڱ�DC�ϣ�������Q�ڱ�DC���ӳ����ϣ�������Q��C���غ�.
���������(1)������P��MN��BC���ֱ�AB��CD�ڵ�M��N�����ı���AMND���ı���BCNM���Ǿ��Σ�
��AMP����CNP���ǵ��������Σ���ͼ1������NP��NC��MB��
�ߡ�BPQ��90����QPN����BPM��90��������BPM����PBM��90����QPN����PBM��
���ߡ�QNP����PMB��90����QNP�ա�PMB��ASA������PQ��PB��
(2)����(1)֪��QNP�ա�PMB����NQ��MP��
��AP��x����AM��MP��NQ��DN��![]() x��BM��PN��CN��1��
x��BM��PN��CN��1��![]() x ��CQ��CD��DQ��1��2��
x ��CQ��CD��DQ��1��2��![]() x��1��
x��1��![]() x
x
��S��PBC��BCBM����1��(1��![]() x)��
x)��![]() ��
��![]() x��
x��
S��PCQ��CQPN����(1��![]() x)(1��
x)(1��![]() x)��
x)��![]() ��
��
��S�ı���PBCQ��S��PBC��S��PCQ��![]() �� ��y��
�� ��y��![]() ��0��x��
��0��x��![]() ����
����
(3)����PCQ���ܳ�Ϊ���������Σ�
������Q�ڱ�DC�ϣ���![]() �ã�
�ã�![]()
���x1��0��x2��![]() (��ȥ)��
(��ȥ)��
������Q�ڱ�DC���ӳ����ϣ���ͼ2������PC��CQ�ã�![]() ��x��
��x��![]() x��1��
x��1��
���x��1��
������Q��C���غϣ���PCQ�����ڣ�
����������x��0��1ʱ����PCQΪ����������