��Ŀ����
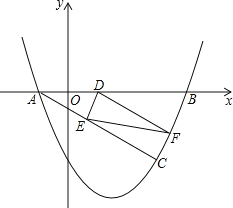
����Ŀ����֪��ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8���Ρ�����ͼ2����ͼ1�������£���DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N���Խ���������⣺
��1����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ��_________��
��2����ϸ�۲죬��ͼ2�С�8���Ρ��ĸ���_________����
��3����ͼ2�У�����D=40�㣬��B=36�㣬�����P�Ķ�����
��4�����ͼ2�С�D�͡�BΪ����ǣ������������䣬���ʡ�P���D����B֮�������������������ϵ��ֱ��д�����ۼ��ɣ�
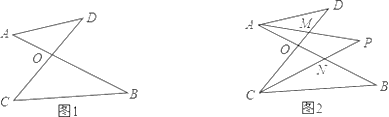
���𰸡�
��1����A+��D=��C+��B
��2��6 ��
��3���⣺��DAP+��D=��P+��DCP ��
��PCB+��B=��PAB+��P ��
�ߡ�DAB����BCD��ƽ����AP��CP�ཻ�ڵ�P
���DAP=��PAB����DCP= ��PCB
��+���ã�
��DAP+��D+��PCB+��B =��P+��DCP+��PAB+��P
���ߡ�D=50�ȣ���B=40��
��50��+40��=2��P
���P=45��
��4����ϵ��2�� P=��D+��B
����������1�������������ڽǺͶ������ɵó���A+��D=��C+��B��
��1��������8�������Ķ��壬��ϸ�۲�ͼ�μ��ɵó���8����������6����
��1���ȸ�����8�������еĽǵĹ��ɣ��ɵ���DAP+��D=��P+��DCP������PCB+��B=��PAB+��P�����ٸ��ݽ�ƽ���ߵĶ��壬�ó���DAP=��PAB����DCP=��PCB������+�����ɵ�2��P=��D+��B�����������P�Ķ�����

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�