题目内容
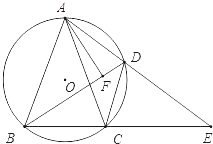
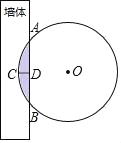
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在墙壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”问题题意为:如图,有一圆柱形木材埋在墙壁中,不知其直径大小.用锯去锯这木材,锯口深1寸(即CD=1寸),锯道长1尺(即AB=1尺),问这圆形木材直径是多少?(注:1尺=10寸)由此,可求出这圆形木材直径为______寸.
【答案】26
【解析】
延长CD,交⊙O于点E,连接OA,由题意知CE过点O,且OC⊥AB,AD=BD=![]() AB=5(寸),设圆形木材半径为r,可知OD=r﹣1,OA=r,根据OA2=OD2+AD2列方程求解可得.
AB=5(寸),设圆形木材半径为r,可知OD=r﹣1,OA=r,根据OA2=OD2+AD2列方程求解可得.
延长CD,交⊙O于点E,连接OA,

由题意知CE过点O,且OC⊥AB,
则AD=BD=![]() AB=5(寸),
AB=5(寸),
设圆形木材半径为r,
则OD=r﹣1,OA=r,
∵OA2=OD2+AD2,
∴r2=(r﹣1)2+52,
解得r=13,
所以⊙O的直径为26寸,
故答案为:26.

练习册系列答案
相关题目
【题目】去学校食堂就餐,经常会在一个买菜窗口前等待,经调查发现,同学的舒适度指数y与等时间x(分)之间满足反比例函数关系,如下表:
等待时间x | 1 | 2 | 5 | 10 | 20 |
舒适度指数y | 100 | 50 | 20 | 10 | 5 |
已知学生等待时间不超过30分钟
(1)求y与x的函数关系式,并写出自变量x的取值范围.
(2)若等待时间8分钟时,求舒适度的值;
(3)舒适度指数不低于10时,同学才会感到舒适.请说明,作为食堂的管理员,让每个在窗口买菜的同学最多等待多少时间?