��Ŀ����
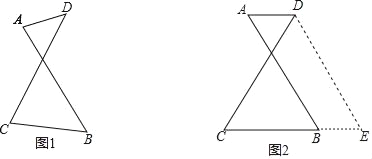
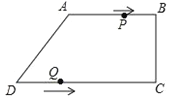
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����BCD=90����AB=AD=10cm��BC=8cm����P�ӵ�A��������ÿ��2cm���ٶ����߶�AB���B�����˶�����Q�ӵ�D��������ÿ��3cm���ٶ����߶�DC���C�˶�����֪����P��Qͬʱ��������P����B����Q����C��ʱ��P��Q�˶�ֹͣ�����˶�ʱ��Ϊt (��)��
��1����CD�ij���
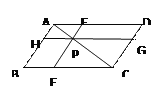
��2�����ı���PBQDΪƽ���ı���ʱ����t��ֵ��
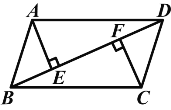
��3���ڵ�P����Q���˶������У��Ƿ����ijһʱ�̣�ʹ��PQ��AB�������ڣ������t��ֵ��˵�����ɣ��������ڣ���˵����

���𰸡���1��16����2��2����3�������ڣ����ɼ�����
����������1����AM��CD��M���ɹ��ɶ�����AM���ٵ�CD=DM+CM=DM+AB��
��2�������⣺BP=AB��AP=10��2t��DQ=3t�����ݣ���BP=DQʱ���ı���PBQD��ƽ���ı��Σ��ɵ�10��2t=3t,����t��
��3����AM��CD��M������PQ��������ڣ���AP=MQ=3t��6����2t=3t��6�������t���������⣬�ʲ�����.
�⣨1����ͼ1����AM��CD��M��
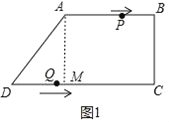
���������ı���ABCM�Ǿ��Σ�
��Rt��ADM��
��DM2=AD2��AM2��AD=10��AM=BC=8��
��AM=![]()
=6��
��CD=DM+CM=DM+AB=6+10=16��
��2�����ı���PBQD��ƽ���ı���ʱ����P��AB�ϣ���Q��DC�ϣ�
��ͼ2�У������⣺BP=AB��AP=10��2t��DQ=3t��
��BP=DQʱ���ı���PBQD��ƽ���ı��Σ�

��10��2t=3t��
��t=2��
��3�������ڣ��������£�
��ͼ3����AM��CD��M������PQ��
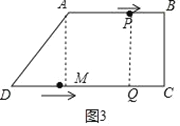
������AP=2t��DQ=3t��
�ɣ�1����֪DM=6����MQ=3t��6��
��2t=3t��6�� ���t=6��
��AB=10��
��t��![]() =5��
=5��
��t=6��5����t=6���������⣬t�����ڣ�

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij������Ʒ�̳��ɹ�ԱҪ�����������������������100ֻ�������ܶ�ó���11 815Ԫ����֪�����ҵ������ۺ��̳������ۼ����ұ����Խ���������⣺
Ʒ�� | ���������ۣ�Ԫ/ֻ�� | �г����ۼۣ�Ԫ/ֻ�� |
���� | 130 | 160 |
���� | 100 | 120 |
��1���òɹ�Ա���ɹ����������ֻ��
��2�������̳�����100ֻ��ȫ�������ۼ��۳���Ϊʹ�̳���õ�������2580Ԫ����ɹ�Ա����Ҫ���������ֻ�����̳�����ӯ������Ԫ��