Question

【题目】如图，矩形边，，沿折叠，使点与点重合，点的对应点为，将绕着点顺时针旋转，旋转角为．记旋转过程中的三角形为，在旋转过程中设直线与射线、射线分别交于点、，当时，则的长为_______．

Answer 1

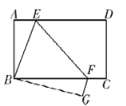
【答案】

【解析】

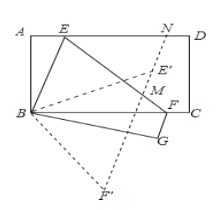
设AE=x=FC=FG，则BE=ED=8-x，根据勾股定理可得：x=，进而确定BE、EF的长，再由折叠性质可得∠BEF=∠DEF=∠BFE和∠DEF=∠NME=∠F'，可证四边形BEMF'为平行四边形，进而得到平行四边形BEMF'为菱形，由菱形的性质可得EM=BE,最后由即可解答．

解：如图：AE=x=FC=FG，则，

在中，有，即，

解得，

，，

由折叠的性质得，

，

，

，，

四边形为平行四边形，

由旋转的性质得：，

，

平行四边形为菱形，

，

．