Question

【题目】如图，△DAC 和△EBC 均是等边三角形，A，C，B 三点在一条直线上，AE，BD 分别与 CD、CE 交于点 M、N，AE，BD 相交于点 O.

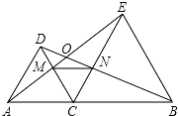
（1）求证：△ACE ≌△DCB;

（2）求∠AOD 的度数

（3）判断△CMN 的形状并说明理由。

Answer 1

【答案】(1)见详解；（2）60°；（3）见详解.

【解析】

（1）欲证三角形全等，利用全等的条件进行判定即可；因为△DAC和△ECB均为等边三角形，即有∠ACD=∠ECB=60°，再注明即可得出∠ACD=∠DCB，利用边的关系，即可得证△ACE≌△DCB；
（2）由全等三角形的性质和三角形的外角性质即可得出结果；

（3）先证△MCE≌△NCB,从而得到MC=NC，再根据有一个角是60°的等腰三角形是等边三角形可判断△CMN 的形状是等边三角形.

（1）证明：∵△DAC是等边三角形，
∴AC=DC，∠ACD=60°，
∵△BCE为等边三角形，
∴CE=CB，∠ECB=60°，
∴∠ACD=∠ECB=60°，
∴∠ACD+∠DCE=∠ECB+∠DCE，
即∠ACE=∠DCB，
在△ACE和△BCD中，

，
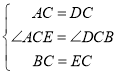∴△ACE≌△DCB（SAS）；

(2)解：∵△ACE≌△DCB，

∴∠AEC=∠ABD.

∵∠AEC+∠BAO=∠BCE=60°

∴∠ABD +∠BAO=∠BCE=60°，

∵∠ABD +∠BAO=∠AOD，

∴∠AOD=60°.

（3）解：△CMN是等边三角形，理由如下：

∵△ACE≌△DCB，

∴∠AEC=∠ABD.

在△MCE和△NCB中，

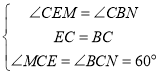
∴△MCE≌△NCB（ASA）

∴CM=CN,

∵

∴△CMN是等边三角形.