题目内容
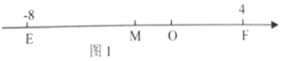
【题目】如图1,在矩形ABCD中,![]() ,
,![]() ,点E从点B出发,沿BC边运动到点C,连结DE,过点E作DE的垂线交AB于点F.
,点E从点B出发,沿BC边运动到点C,连结DE,过点E作DE的垂线交AB于点F.
![]() 求证:
求证:![]() ;
;
![]() 求BF的最大值;
求BF的最大值;
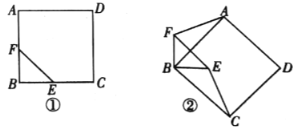
![]() 如图2,在点E的运动过程中,以EF为边,在EF上方作等边
如图2,在点E的运动过程中,以EF为边,在EF上方作等边![]() ,求边EG的中点H所经过的路径长.
,求边EG的中点H所经过的路径长.

【答案】(1)证明见解析;(2)当![]() 时,BF存在最大值
时,BF存在最大值![]() ;(3)点H所经过的路径长是
;(3)点H所经过的路径长是![]() .
.
【解析】分析:(1)依据∠BFE+∠BEF=90°,∠CED+∠BEF=90°,即可得到∠BFE=∠CED,再根据∠CED=∠ADE,即可得出∠BFE=∠ADE;
(2)依据△BEF∽△CDE,即可得到![]() ,设BE=x(0≤x≤3),则CE=3-x,根据BF=
,设BE=x(0≤x≤3),则CE=3-x,根据BF=![]() ,即可得到当x=
,即可得到当x=![]() 时,BF存在最大值
时,BF存在最大值![]() ;
;
(3)连接FH,取EF的中点M,连接BM,HM,依据BM=EM=HM=FM,可得点B,E,H,F四点共圆,连接BH,则∠HBE=∠EFH=30°,进而得到点H在以点B为端点,BC上方且与射线BC夹角为30°的射线上,再过C作CH'⊥BH于点H',根据点E从点B出发,沿BC边运动到点C,即可得到点H从点B沿BH运动到点H',再利用在Rt△BH'C中,BH'=BCcos∠CBH'=3×![]() =
=![]() ,即可得出点H所经过的路径长是
,即可得出点H所经过的路径长是![]() .
.
详解:![]() 证明:如图1,在矩形ABCD中,
证明:如图1,在矩形ABCD中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 由
由![]() 可得,
可得,![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
在矩形ABCD中,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,BF存在最大值
时,BF存在最大值![]() ;
;
![]() 如图2,连接FH,取EF的中点M,连接BM,HM,
如图2,连接FH,取EF的中点M,连接BM,HM,
在等边三角形EFG中,![]() ,H是EG的中点,
,H是EG的中点,
![]() ,
,![]() ,
,
又![]() 是EF的中点,
是EF的中点,
![]() ,
,
在![]() 中,
中,![]() ,M是EF的中点,
,M是EF的中点,
![]() ,
,
![]() ,
,
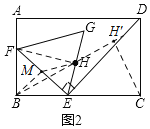
![]() 点B,E,H,F四点共圆,
点B,E,H,F四点共圆,
连接BH,则![]() ,
,
![]() 点H在以点B为端点,BC上方且与射线BC夹角为
点H在以点B为端点,BC上方且与射线BC夹角为![]() 的射线上,
的射线上,
如图,过C作CH'⊥BH于点H',
∵点E从点B出发,沿BC边运动到点C,
∴点H从点B沿BH运动到点H',
在Rt△BH'C中,∠BH'C=90°,
∴BH'=BCcos∠CBH'=3×![]() =
=![]() ,
,
![]() 点H所经过的路径长是
点H所经过的路径长是![]() .
.

【题目】为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市民一户一表"生活用水阶梯式计费价格表的部分信息:
自来水销售价格 | 污水处理价格 | |
每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
|
|
|
超过 |
|
|
超过 |
|
|
(说明:每户生产的污水量等于该户自来水用量;②水费=自来水费用+污水处理费)
已知小王家2018年7月用水![]() 吨,交水费
吨,交水费![]() 元.8月份用水
元.8月份用水![]() 吨,交水费
吨,交水费![]() 元.
元.
(1)求![]() 的值;
的值;
(2)如果小王家9月份上交水费![]() 元,则小王家这个月用水多少吨?
元,则小王家这个月用水多少吨?
(3)小王家10月份忘记了去交水费,当他11月去交水费时发现两个月一共用水50吨,其中10月份用水超过![]() 吨,一共交水费
吨,一共交水费![]() 元,其中包含
元,其中包含![]() 元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
元滞纳金,求小王家11月份用水多少吨? (滞纳金:因未能按期缴纳水费,逾期要缴纳的“罚款金额”)
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?